Hallo,
mein Thema ist etwas schwer einzuordnen- versuche es hier, denn ich baue ein "Modell" und müsste folgendes Berechnen:
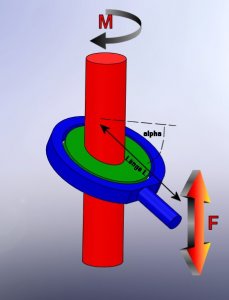
Gesucht ist das benötigte Drehmoment M, um eine Kraft F am blauen Hebel auszuüben.
Dabei ist grün und rot fest miteinander verbunden. Grün und blau aber gegeneinander verdrehbar (Wälzlager z.B.). Der Hebel dreht nicht mit- kann sich nur vertikal bewegen.
Wer weiß Rat? Wie geht man sowas an?
Frohes Fest wünsche ich!
Gruß
David
mein Thema ist etwas schwer einzuordnen- versuche es hier, denn ich baue ein "Modell" und müsste folgendes Berechnen:
Gesucht ist das benötigte Drehmoment M, um eine Kraft F am blauen Hebel auszuüben.
Dabei ist grün und rot fest miteinander verbunden. Grün und blau aber gegeneinander verdrehbar (Wälzlager z.B.). Der Hebel dreht nicht mit- kann sich nur vertikal bewegen.
Wer weiß Rat? Wie geht man sowas an?
Frohes Fest wünsche ich!
Gruß
David

 aber hier kommt der cosin in Spiel.
aber hier kommt der cosin in Spiel.
