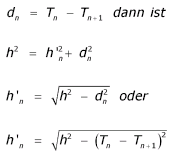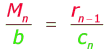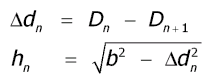Manch einer fragt sich vielleicht bereits jetzt schon: Wie um alles in der Welt, kommt man nur auf die Idee, eine Kugel abwickeln zu wollen? Das braucht doch kein Mensch! So dachte ich auch. Allerdings nur so lange, bis ich eines schönen Tages die Mail des Users Christof H. mit folgendem Inhalt erhielt: „Hallo, wie funktioniert die Abwicklung bei einer halben Kuppel? Also ein Viertelkreis als Kuppel. Ich konnte es einmal aber ich krieg es einfach nicht mehr hin“!
Da dämmerte es mir: „Wenn sich einer mit so einem Problem vergeblich abmüht, gibt’s möglicherweise auch noch andere, die nach einer Antwort suchen.“ Das war schließlich der Anlass, zu versuchen, die Abwicklung einer Kugel so einfach und durchschaubar wie möglich zu erläutern, damit auch der Ungeübteste zielsicher zu einer angenäherten Abwicklung kommt. Nach etwas Internetrecherche bin ich auf zwei Methoden für die Lösung dieses Problems gestoßen.
Als Ergänzung der bereits an anderer Stelle beschriebenen Konstruktion der Abwicklung eines Übergangskörpers möchte ich in dieser Anleitung zwei Methoden zur näherungsweisen Abwicklung von Kugeloberflächen vorstellen. Die Einschränkung "näherungsweise" gilt deshalb, weil es grundsätzlich nicht möglich ist, die dreidimensionale Kugeloberfläche exakt auf einer zweidimensionalen Fläche abzubilden. Es ist zwar möglich, beispielsweise ein flächengleiches Quadrat zu zeichnen, aber es gelingt mit keinem Trick dieser Welt, dieses Quadrat zu einer Kugel mit gleicher Oberfläche zu formen.
Um aber gleich allen Missverständnissen vorzubeugen: Diese Methoden sind keinesfalls als die Ultima Ratio oder als Königsweg anzusehen. Es gibt sicher noch andere und auch bessere Verfahren. Mir erschienen diese Beiden lediglich bezüglich der handwerklichen Anforderungen die Sinnvollsten, um Gelegenheitsabwickler wie Dich und mich in die Lage zu versetzen, mal eine Kugel halbwegs zuverlässig und mit überschaubarem Aufwand abwickeln zu können!
Aber genug der Vorrede, es geht ab sofort nur noch um...
Mäntel, Apfelsinenspalten und stumpfe Kegel
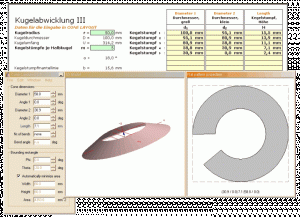
Zu Beginn und für die ungeduldigsten Gemüter wird in Teil I und II gezeigt, wie schnellstens die benötigten Größen für beide Methoden jeweils mit Hilfe von vorgefertigten EXCEL-Sheets ermittelt werden können. Dabei beschränke ich mich zunächst auf die reine Darstellung der Tabellen und auf Hinweise, welche Werte in welche Zellen eingegeben werden müssen und wo die Ergebnisse abzulesen sind.
Im Teil III wird dann zunächst die konventionelle Arbeitsweise mit Bleistift, Lineal und Zirkel beschrieben, bei der man gänzlich ohne Rechnerunterstützung auskommt und anschließend die rechnerische Behandlung der gestellten Aufgabe, die letztlich zu den Ergebnissen unter EXCEL verhelfen.
Ich werde diese Rechenschritte im Einzelnen erläutern, aber dennoch versuchen, alles so knapp und übersichtlich wie möglich zu halten.
Schließlich gehe ich noch kurz auf die Verwendung der CONE LAYOUT-Software ein, für die ich auch ein EXCEL-Sheet zur Berechnung der erforderlichen Kegelabmessungen anbiete.
Anmerkung: CONE LAYOUT ist eine reine Kegelmantelabwicklungs-Software, hat also rein gar nichts mit Kugelabwicklung zu tun. Sie erspart lediglich das manuelle Konstruieren und Zeichnen von Kegelmantelabwicklungen!
Teil I
- Kugel entlang von Längenkreisen bzw. Großkreisen aufteilen (Apfelsinenspaltenverfahren),
- die Eingaben in die EXCEL-Tabelle I (Abb.25)
Teil II
- Kugel in äquatorparallele Scheiben aufteilen (Kegelstumpfverfahren),
- die Eingaben in die EXCEL-Tabelle II (Abb.26)
Teil III
- Geometrische Konstruktion zu I
- Rechnerische Ermittlung zu I
- Geometrische Konstruktion zu II
- Rechnerische Ermittlung zu II
- Eingaben für CONE LAYOUT (EXCEL-Sheet III, Abb.27)
Teil I
Apfelsinenspaltenverfahren
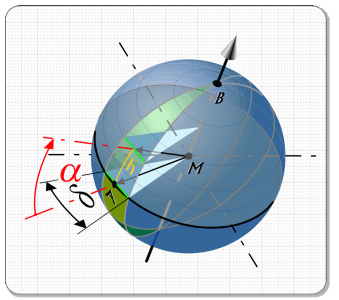
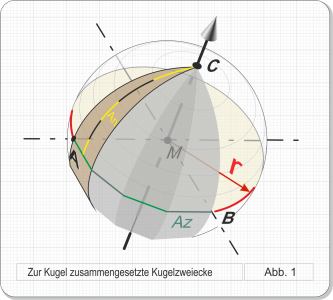
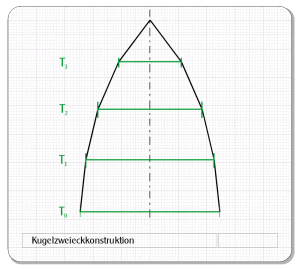
So, wie sich eine Apfelsine in einzelne Spalten zerlegen lässt, kann man sich auch die Zerlegung einer Kugel in mehrere „Spalten“ vorstellen, wenn man sie entlang ihrer Großkreise, Längenkreise oder Meridiane aufschneiden würde. Wir benötigen von diesen „Spalten“ nur die äußere Fläche, in Abb. 1 braun eingefärbt. Die gesamte Kugel besteht natürlich aus mehreren dieser Flächen. Aber da alle diese Flächen identisch sind, reicht es, die Abmessungen einer Fläche, des sogenannten Kugelzweiecks, zu kennen. Noch besser: Das Kugelzweieck ist symmetrisch, d. h. der Teil auf der „Nordhalbkugel“ ist gleich der Hälfte auf der „Südhalbkugel“. Das vereinfacht uns die Sache noch einmal erheblich. Die erforderlichen Abmessungen entnehmen wir der EXCEL-Tabelle I (Abb. 2 und Abb. 25).
Abb. 1
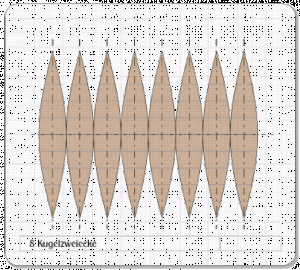
Abb. 1a
Diese acht Kugelzweiecke entsprechen der abgewickelten halben, oben (Abb. 1) dargestellten, Kugel.
Die Eingaben in die EXCEL-Tabelle Kugelabwicklung I (Abb. 25) beschränken sich auf bescheidene drei Größen:
Abb. 2
1. Den Radius r der abzuwickelnden Kugel,
2. die gewünschte Anzahl k der Zweiecke (für gesamten Kugelumfang) und
3. die gewünschte Anzahl m der Zweieckabschnitte (horizontale Teilung einer Zweieckhälfte).
Ablesen können wir anschließend:
1. die Höhe h der Zweieckabschnitte sowie
2. die Breiten des Kugelzweiecks T0 bis Tn.
Wie aus diesen Größen das Kugelzweieck konstruiert werden kann, wird ebenso Schritt für Schritt im Teil III erläutert, wie auch die Vorgehensweise, um selbst ohne EXCEL die benötigten Angaben zu erhalten!
Teil II
Kegelstumpfverfahren
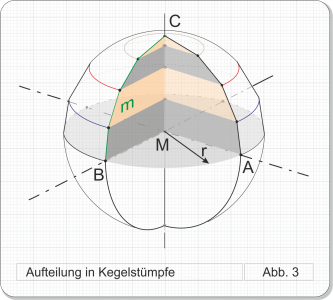
Die abzuwickelnde Kugel wird nun nicht wie unter I. senkrecht zum Äquator geschnitten, sondern parallel zu ihm. Die so entstehenden Scheiben werden vereinfachend als Kegelstümpfe betrachtet und wie solche abgewickelt.
Abb. 3
Die Eingaben in die EXCEL-Tabelle II:
Zur Bestimmung der Abmessungen der verschiedenen Kegelstümpfe sind folgenden beiden Größen in die EXCEL-Tabelle einzutragen (Abb. 4 und Abb. 26):
Abb. 4
1. Der Radius r und
2. die Anzahl m der „Scheiben“ bzw. Kegelstümpfe einer Halbkugel.
Ablesen können wir anschließend:
1. die Länge der Kegelmantellinie Mn,
2. die Länge der Kegelstumpfmantellinie b und
3. der Zentriwinkel γn.
Schließlich gibt es noch mindestens ein weiteres Verfahren, eine Kugel abzuwickeln. Das ist aber sowohl von der rechnerischen Seite als auch was die praktische Ausführung betrifft etwas komplizierter.
Teil III
a) Geometrische Konstruktion zu I (Apelsinenspaltenverfahren)
Es soll die Oberfläche einer Kugel mit dem Durchmesser D abgewickelt werden. Dazu wird ein Verfahren gewählt, bei dem die Kugel in mehrere „Apfelsinenspalten“ aufgeteilt wird. Die „Außenhaut“ dieser Teilkörper wird vereinfachend als eindimensional gekrümmt angesehen, um sie in der Ebene abwickeln zu können (Abb. 1).
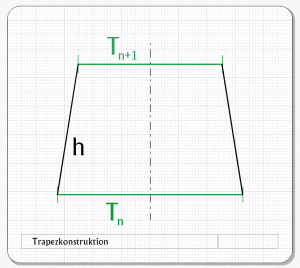
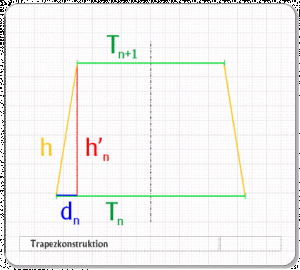
Zur Konstruktion des halben Kugelzweiecks (an T0 horizontal gespiegelt ergibt ein Ganzes), das man sich vereinfacht aus symmetrischen Trapezen zusammengesetzt vorstellen kann (Abb. 5), ist die Kenntnis folgender Abmessungen erforderlich (Abb. 6):
Die Trapezseite h sowie die untere und obere horizontale Seite Tn und Tn+1.
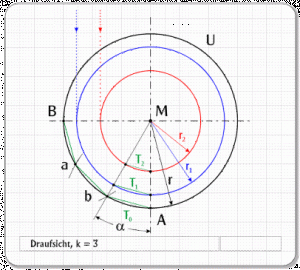
Gehen wir beispielhaft davon aus, dass wir unsere Kugeloberfläche in 12 Kugelzweiecke aufteilen und diese abwickeln wollen. Dazu teilen wir in der Draufsicht den Umfang U der Kugel, also den Kugeläquator, in 12 gleiche Abschnitte ein. Je Kreisviertel ergibt das drei Abschnitte, Ab, ba und aB, wie in Abb. 7 gezeigt.
Die Punkte a und b ergeben sich aus den Schnittpunkten der Kreise mit dem Radius r um A und B. Der Einfachheit halber beschränke ich mich auf die Darstellung eines Kreisviertels. Die Punkte auf dem übrigen Kreisumfang konstruiert man entsprechend.
Verbindet man nun die Punkte A und b mit einer Geraden, erhält man eine Sehne des Kreises um M. Dies ist die größte Breite T0 des Kugelzweiecks. Natürlich kann man T0 auch rein rechnerisch mit dem Sehnensatz ermitteln.
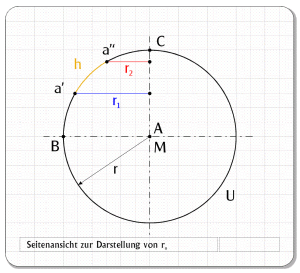
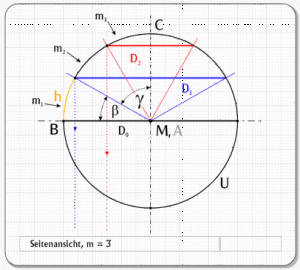
Um weitere T bestimmen zu können, betrachten wir die Seitenansicht der Kugel. (Abb. 8)
Den Kugelumfang teilen wir in der Seitenansicht in gleichgroße Kreisabschnitte ein. Wie wir dabei vorgehen ist ohne Belang. Die Anzahl sollte aber ohne Rest durch 4 teilbar sein, damit sie exakt auf einen Viertelkreis passen. Im oben dargestellten Beispiel habe ich rein willkürlich erneut 12 Abschnitte gewählt, betrachtet wird aber nur ein Kreisviertel, das in drei Abschnitte aufgeteilt wurde. Ihr wisst schon, Einfachheit ist Trumpf und die Symmetrie erleichtert uns das Leben!
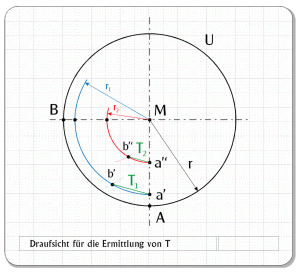
Horizontale Geraden durch die Punkte a’ und a’’ ergeben die Strecken r1 und r2. Die Bezeichnung r bietet sich an, da es sich hier auch wieder um Kreisradien handelt. Mit diesen Radien zeichnen wir in der Draufsicht jeweils einen Kreis um den Mittelpunkt M (Abb. 9).
Die Punkte b’ und b’’ konstruieren wir wie die Punkte a und b in Abb. 9. Die Sehnen a’b’ und a’’b’’ sind die Trapezseiten T1 und T2 . Für die Konstruktion des symmetrischen Trapezes fehlt uns nur noch die Länge der Seite h. Diese Abmessung ergibt sich aus der Tatsache, dass wir oben die Seitenansicht der Kugel (Kreis) in 12 Abschnitte aufgeteilt haben. Daher gilt
für h = U/12
mit U = 2 * π * r
und π = 3,14159
Wie konstruiert man jetzt daraus eine (halbe) Apfelsinenspalte?
Die Konstruktion in 11 Schritten:
Schritt 1:
Eine Senkrechte m zeichnen (Mittellinie).
Schritt 2:
Am unteren Ende von m wird im rechten Winkel die Strecke T0 eingezeichnet.
Schritt 3:
Ebenfalls dort und symmetrisch zu m wird die Strecke T1 angetragen.
Schritt 4:
An den Endpunkten der Strecke T1 jeweils die Senkrechten s1 errichten.
Schritt 5:
Um einen Endpunkt der Strecke T0 einen Kreisbogen mit dem Radius h schlagen.
Schritt 6:
Durch den Schnittpunkt des Kreisbogens mit s1 die Horizontale g1 zeichnen.
Schritt 7:
Auf g1, symmetrisch zur Mittellinie m, die Strecke T2 antragen.
An den Endpunkten von T2 jeweils die Senkrechten s2 errichten.
Schritt 8:
Um den Schnittpunkt von g1 mit s1 einen Kreisbogen mit dem Radius h schlagen.
Schritt 9:
Durch den Schnittpunkt des Kreisbogens mit s2 die Horizontale g2 zeichnen.
Schritt 10:
Auf g2, symmetrisch zur Mittellinie m, die Strecke T3 antragen.
An den Endpunkten von T3 jeweils die Senkrechten s3 errichten.
Diese Abfolge so oft wiederholen, bis alle Strecken T0 bis Tn „verarbeitet“ sind.
Schritt 11:
Anschließend alle Mittelpunkte der Kreisbögen verbinden und die Kontur des entstandenen Polygons vervollständigen und etwas glätten. Das Ergebnis ist ein halbes Kugelzweieck.
b) Rechnerische Ermittlung zu I
Gegeben: Eine Kugel mit dem Durchmesser D bzw. Radius r mit r = D/2,
die Teilung m eines Kreisviertels des Großkreises,
die Teilung k des Kreisumfangs (Äquatorebene).
Gesucht: Die Trapezseiten Tn und h (Abb. 10).
m sei die Anzahl der Trapeze bzw. Zweiecksabschnitte im Kreisviertel. Mit n wird die Laufvariable bezeichnet: n = 1 ... m
Abb. 11 können wir entnehmen:
(1)
also folgt für
(2)
oder
(3)
letztlich ist
(4)
Die Durchmesser (Sehnenlängen) Dn ergeben sich aus:
(5)
Nach dem gleichen Verfahren werden die Breiten Tn der Kugelzweiecke bestimmt, die ebenfalls Sehnen der Kreise mit dem Durchmesser Dn bzw. mit dem Radius rn sind.
k ist die Anzahl der Abschnitte in die der Kreisumfang aufgeteilt worden ist.
Nach Voraussetzung ist
(6)
damit folgt für
(7)
Wir leisten uns den Luxus und setzen alles ein. Dann ergibt sich für Tn:
(8)
Nur der Vollständigkeit wegen (die Kenntnis der Länge von h' ist entbehrlich, da h bereits bekannt ist):
Bei der geometrischen Konstruktion ergibt sich die Trapezhöhe h’ quasi „automatisch“. Die rechnerische Ermittlung gestaltet sich recht einfach mittels Pythagoras:
(9)
Die Länge der Trapezseite h ergibt sich aus dem Kreisumfang U geteilt durch die gewählte Anzahl m der Kreisabschnitte!
c) Geometrische Konstruktion zu II (Kegelstumpfverfahren)
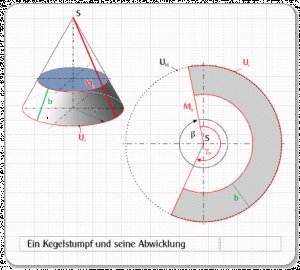
Es soll die Oberfläche einer Kugel mit dem Durchmesser D = 2 r abgewickelt werden. Dazu wird ein Verfahren gewählt, bei dem die Kugel in mehrere äquatorparallele „Scheiben aufgeteilt wird. Diese Teilkörper werden vereinfachend als Kegelstümpfe angesehen, um sie in der Ebene abwickeln zu können (Abb. 3, Abb. 14).
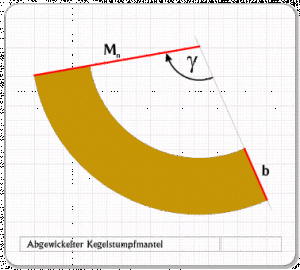
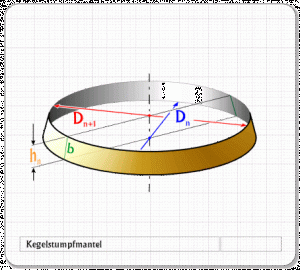
Dies ist das prinzipielle Aussehen eines abgewickelten Kegelstumpfs (Abb. 15). Wie man erkennen kann, ist für die geometrische Konstruktion der Abwicklung die Kenntnis von drei Größen erforderlich.
Im Einzelnen sind dies:
1. Die Kegelmantellinie Mn,
2. die Kegelstumpfmantellinie b sowie
3. der Mittelpunkts- oder Zentriwinkel γ.
Für die Bestimmung dieser Größen kann man sich auf die Darstellung eines Kreisviertels beschränken, da aus diesem bereits fast alle für die geometrische Konstruktion relevanten Größen abgegriffen werden können. Lediglich der Zentriwinkel γ muss berechnet werden.
Aus der Anzahl m der für die Halbkugel gewählten Kegelstümpfe (Abb. 3) ergibt sich der Winkel α zu
α = 90°/m
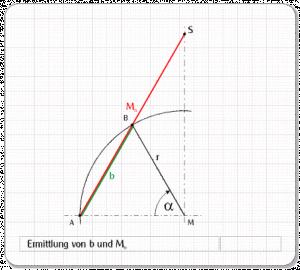
Trägt man diesen Winkel wie in Abb. 16 in die Zeichnung des Kreisviertels ein, ergibt sich der Schnittpunkt B mit dem Kreisbogen. Die Strecke AB ist die Länge der gesuchten Kegelstumpfmantellinie b.
Verlängert man b über B hinaus bis zum Schnittpunkt S mit der Mittellinie, erhält man mit der Strecke AS die Länge der Kegelmantellinie Mn.
Die noch fehlende Größe, den Zentriwinkel γ, berechnen wir aus folgender Betrachtung:
Der Umfang Ur des Kreises mit dem Radius r verhält sich zum Umfang UM des Kreises mit dem Radius Mn wie der Zentriwinkel γn zu β (Abb. 17).
Mit
(10)
folgt
(11)
oder
(12)
Daraus ergibt sich für
(13)
Damit sind alle erforderlichen Größen für eine geometrische Konstruktion der Abwicklung eines Kegelstumpfmantels bestimmt.
d) Rechnerische Ermittlung zu II
Gegeben: Eine Kugel mit dem Radius r bzw. dem Durchmesser D mit D = 2r,
die Teilung einer Halbkugel in m Kegelstümpfe (Abb. 16).
Gesucht: Die Länge der Kegelmantellinie Mn, die Länge der Kegelstumpfmantellinie b und der Zentriwinkel γn (Abb. 17).
Die Kegelstumpfmantellinie b ist für alle Kegelstümpfe gleich, da laut Voraussetzung der Viertelkreis in m gleiche Abschnitte geteilt wurde (Abb. 18). Für den Winkel α gilt: α = 90°/m (Abb. 16).
Die Sehne des Kreises mit dem Radius r =D/2 ist die Kegelstumpfmantellinie b, deren Länge sich ergibt aus:
(14)
Gesucht ist die Länge von Mn?
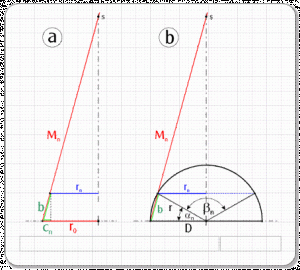
Diese Frage lässt sich beispielweise mit Hilfe der Ähnlichkeit der in rot und grün dargestellten Dreiecke beantworten (Abb. 19a).
Der Winkel αn ergibt sich zu αn = n * 90°/m, demzufolge ist der Winkel βn = 180° - 2 αn,
außerdem ist r0 = r
Aus Abb. 19a entnehmen wir:
(15)
mit
(16)
außerdem gilt
(17)
daraus folgt
(18)
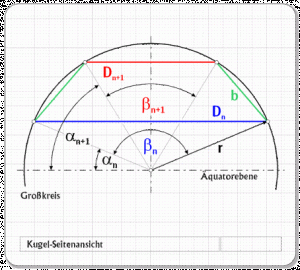
Die noch fehlende Größe, den Zentriwinkel γ, berechnen wir aus folgender Betrachtung:
Der Umfang Ur des Kreises mit dem Radius r verhält sich zum Umfang UM des Kreises mit dem Radius Mn wie der Zentriwinkel γn zu β (Abb. 17).
Mit
(10)
folgt
(11)
oder
(12)
Daraus ergibt sich für
(13)
[PAGE][/PAGE]
e) Eingaben für CONE LAYOUT (EXCEL-Sheet III)
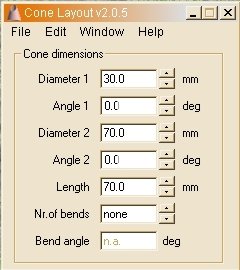
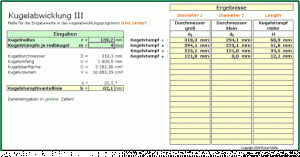
Die CONE LAYOUT–Software benötigt zur Berechnung der Abwicklung die Eingabe folgender Kegelstumpfabmessungen:
- Großer Durchmesser des Kegelstumpfs (Diameter 1),
- kleiner Durchmesser des Kegelstumpfs (Diameter 2),
- die Höhe des Kegelstumpfs (Length),
- die beiden Winkel (Angle 1, Angle 2) belassen wir bei 0°.
(19)
m ist die Anzahl der Kegelstümpfe pro Halbkugel.
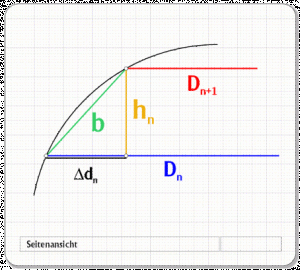
Diameter 1: Dn
(20)
Diameter 2: Dn+1
(21)
Length: hn
(22)
Zur Verdeutlichung, um was es in Abb. 22 geht:
Die für die beschriebenen Verfahren erstellten EXCEL-Tabellen I bis III gibt es auf Anforderung kostenlos (eine kleine Spende via PayPal wäre aber dennoch toll) von mir per E-Mail. Anfragen bitte an: eckart.mueller@gmx.de.
Vielleicht habe ich mit diesen Beschreibungen dem Einen oder Anderen bei der Lösung seiner Probleme etwas helfen können. Das würde mich freuen! Falls sich Passagen finden, die ich nicht deutlich genug erklärt habe, reicht eine Anfrage per Mail an mich. Ich versichere, so schnell wie möglich zu antworten.
Es ist trotz aller Sorgfalt leider nie auszuschließen, dass sich Tipp- oder andere Fehler im Text oder in den Formeln eingeschlichen haben. Falls Du also irgendwelche Ungereimtheiten findest, wäre ich für einen Hinweis dankbar. Folglich übernehme ich keine Gewähr für Fehlerfreiheit. Selbstverständlich hafte ich nicht für Folgen, die sich aus der Verwendung dieser Anleitungen ergeben sollten.
Und jetzt wünsche ich allen, die es bis hier hin ausgehalten haben, ein fröhliches und erfolgreiches Abwickeln!
Dieser Text steht auch als Word-Dokument zur Verfügung und kann bei Interesse von mir per Mail bezogen werden.
Und wer wegen einer Kugelabwicklung nicht gleich CONE LAYOUT kaufen will, dem kann ich die Kegelstumpfabwicklungen als eps- oder dxf-File schicken!
Nachtrag: Ich bin mir darüber im Klaren, dass die Apfelsinenmethode eklatante Schwächen hat. Genaugenommen kann die abzuwickelnde Kugel einzig und alleine durch einen Körper angenähert werden, dessen Oberfläche aus zahlreichen ebenen Trapezen gebildet wird. Dabei sind alle Trapezseiten Sehnen der Kugel mit Ausnahme der Trapezhöhe. Das wird vielleicht mal in einem Teil IV behandelt werden, inklusive der Berechnung mittels EXCEL-Sheet! Vielleicht wird aber auch nur der Teil I umgearbeitet...
Auch das Kegelstumpfverfahren bietet noch Variationsmöglichkeiten. Statt mit Kegelstümpfen konstanter Höhe zu arbeiten, bei denen die Mantelbreite zum Pol hin zunimmt, könnte man beispielsweise die Abwicklung so anlegen, dass die Mantelbreite konstant bleibt. Für die eigene Kreativität gibt es also noch reichlich Spielraum!
Zuletzt bearbeitet: