von Otto Jakob
Ein kleiner Ausflug in die Physik unserer Atmosphäre
Wir Modellflieger haben einen ganz besonderen Bezug zu Wind und Wetter. Etwas allgemeiner: Zu der unteren Schicht unserer Atmosphäre, die nicht nur unser Leben sondern auch das Modellfliegen erst ermöglicht.
Die Atmosphäre ist für alle gleich. Die Hummel bewegt sich im gleichen Medium wie ein Airbus solange beide in der gleichen Höhe fliegen. Wenn die Hummel ihre Dienstgipfelhöhe erreicht hat, hat sie etwa die gleichen atmosphärischen Bedingungen wie der Airbus im Landeanflug.
Das Medium Luft will ich im folgenden Aufsatz dem -User etwas näher bringen. Die Luftdichte ist z. B. bei Leistungsmessungen an Luftschrauben zu beachten. Die Speedflieger wollen ihre Messungen bei unterschiedlichen Bedingungen diskutieren, usw...
-User etwas näher bringen. Die Luftdichte ist z. B. bei Leistungsmessungen an Luftschrauben zu beachten. Die Speedflieger wollen ihre Messungen bei unterschiedlichen Bedingungen diskutieren, usw...
Auftrieb und Widerstand, welche Rolle spielt die Luftdichte?
Da fällt mir doch mein Lieblingsspruch ein:
Beide Kräfte sind direkt proportional zur Luftdichte.
Zur Berechnung dieser Kräfte wurden folgende Gleichungen aufgestellt:
Auftrieb = Staudruck ⋅ Auftriebsbeiwert ⋅ Bezugsfläche
Widerstand = Staudruck ⋅ Widerstandsbeiwert ⋅ Bezugsfläche
Die Bezugsfläche könnte beliebig definiert werden. Bei Flugzeugen hat man sich darauf geeinigt, als Bezugsfläche die Flügelfläche zu nehmen. Die Beiwerte sind dimensionslos und deswegen universell verwendbar. Der Auftriebsbeiwert cA und der Widerstandsbeiwert cW sind bekannte Größen, die wir z. B. aus der Flugzeugpolaren ablesen können.
Für erste Abschätzungen können wir mit cA = 1 und cW = 0,1 arbeiten. Dieses Flugzeug hätte also eine Gleitzahl cA/cW = 10. Je nach Konfiguration können diese Werte sowohl nach oben als auch nach unten überschritten werden.
Der Staudruck ist definiert als:
Staudruck q = 0,5 ⋅ Luftdichte ⋅ Geschwindigkeit ⋅ Geschwindigkeit
Wichtig für uns ist: Die Luftkräfte, also Auftrieb und Widerstand, hängen linear von der Luftdichte und quadratisch von der Geschwindigkeit ab.
Die Dichte der Luft
Jedes Medium, egal ob fest, flüssig oder gasförmig, hat eine Dichte. Sie ist definiert als Masse/Volumen. Gebräuchlich ist z. B. die Masse für 1 m³ (ein Würfel mit 1 m Kantenlänge) eines Stoffs anzugeben.
Wir wissen noch:
1 m3 Wasser hat eine Masse von 1000 kg, also Wasser hat die Dichte (rho) ρWasser = 1000 kg/m3. Die Masse für einen dm3 oder Liter (l) Wasser ist „griffiger“ und damit leichter zu merken. 1 l Wasser hat eine Masse von 1 kg.
Umgangssprachlich dürfen wir auch sagen 1 l Wasser wiegt 1 kg. Genau genommen wiegt 1 l Wasser 9,81 N, das ist die Gewichtskraft, die 1 kg Masse ausübt.
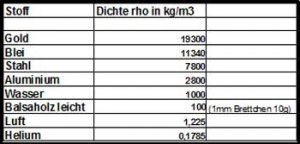
Hier ein paar Werte für andere Stoffe:
Anekdote:
Der kleine Otto wollte die Flugleistung seines Amigo steigern und füllte deswegen seinen folienbespannten Flügel mit Helium. Vom Testflug mit dem Heliumflügel kam er sehr enttäuscht zurück. Er konnte keinen Unterschied feststellen, und eine kleine Rechnung zeigt warum:
Der Flügel hat ein Volumen von ca. 0,003 m3 . Der Auftrieb von 1 m3 Helium beträgt ca. 1,05 kg. Da der Flügel aber nur ein sehr kleines Volumen hat, beträgt der statische Auftrieb auch nur ca. 3 g.
Der Amigoflügel mit Heliumfüllung ist deswegen nur 3 g leichter als ein Flügel mit Luft drin.
Die Dichte der Luft ist nicht konstant, sondern von verschiedenen Parametern abhängig.
Da wir in der Technik für Alles eine Norm erstellen, wurde auch ein Modell der Atmosphäre erstellt. Diese Norm heißt DIN ISO 2533 und beschreibt die sog. „Standardatmosphäre“. Der obige Wert von 1,225 kg/m3 für die Luftdichte ist der Normwert bei einer Temperatur von 15°C und einem Druck von 1013,25 hPa.
Wovon hängt die Luftdichte ab?
Die Dichte der Luft hängt in erster Linie vom Druck und von der Temperatur ab. Später nehmen wir den Einfluss der Luftfeuchte hinzu. Die Verhältnisse werden durch die allgemeine Gasgleichung beschrieben:
(diese Gleichung ist sehr wichtig, und für alle Techniker lohnt es, sich so etwas zu merken!)
Dichte Luft = Druck / (Temperatur ⋅ Gaskonstante)
Wichtig:
Wie stark schwankt der Luftdruck?
Bei der Änderung des Luftdrucks müssen wir zwei Fälle unterscheiden:
*Es gibt zwar Gegenden, die unter NN liegen aber praktisch hat das keine Bedeutung.
Der Korrekturterm durch die Höhe wird später erläutert.
Der höchste gemessene Luftdruck in Deutschland betrug 1056,6 hPa. Die höchste gemessene Druckabnahme ca. 100 hPa in 23 h. Der niedrigste Wert liegt bei etwa 856 hPa. Daraus schließen wir, dass sich der Luftdruck um etwa ±5% ändert, und demzufolge sich die Luftdichte durch den Druck auch im gleichen Verhältnis ändert.
Luftdichteänderung durch Temperaturänderung
Wie wir in der allgemeinen Gasgleichung gesehen haben, ist die Luftdichte linear mit der Temperatur verknüpft.
Wichtig: Die Temperatur muss in K eingesetzt werden.
Ich persönlich gehe normalerweise nur bei Temperaturen über 0°C zum Fliegen. Im Sommer oberhalb von 30°C, also bei 303 K wird die Sache sehr schweißtreibend, und es gibt angenehmere Freizeitgestaltungen, z. B. Baden im Bodensee.
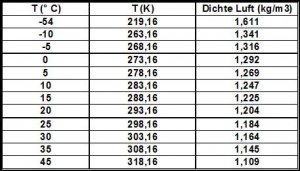
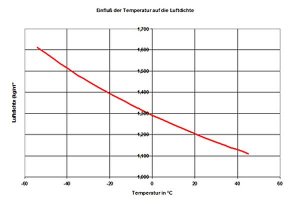
Um den Einfluss der Temperatur darzustellen, berechnen wir ein paar Werte für Normaldruck: 101325 Pa.
Betrachten wir den Bereich zwischen -5°C und +30°C stellen wir fest, dass sich in diesem Bereich die Luftdichte um ca. 11,5% ändert.
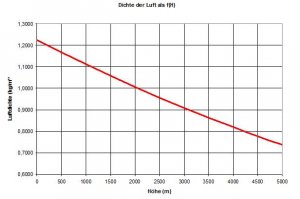
Abhängigkeit der Dichte von der Flughöhe
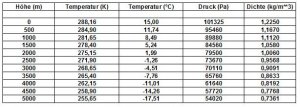
Im Modell der Normatmosphäre wird eine Temperaturabnahme von 6,5 K pro 1000 m Höhendifferenz im Bereich zwischen 0 und 11 km Höhe festgelegt. Aus der allgemeinen Gasgleichung und der statischen Grundgleichung der Atmosphäre lässt sich daraus die Änderung der Dichte mit der Höhe beschreiben.
Auswirkung in der Praxis:
Eine Starthöhe von 2000 bis 2500 m ist in den alpinen Fluggebieten durchaus üblich. Eine Startüberhöhung von 500-1000 m je nach Größe des Flugmodells ist möglich (wenn auch nicht immer legal). In dieser Höhe ist die Luftdichte schon deutlich niedriger als am Boden.
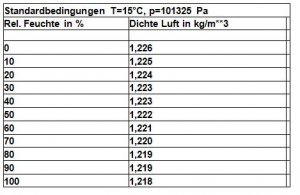
Einfluss der Feuchte auf die Dichte
Jeder Student oder Schüler ist schon über die Frage gestolpert: Was ist leichter, trockene oder feuchte Luft?
Die richtige Antwort lautet: Feuchte Luft ist leichter als trockene Luft!
Für uns Modellflieger ist das sehr wichtig. Warme, feuchte Luft steigt nach oben, und wir nutzen diese aufsteigende Luftmasse als Thermik. Wenn feuchte Luft nicht leichter wäre, würden sich keine Wolken bilden.
Die Zusammenhänge sind nicht so trivial. Im Internet sind EXCEL-Programme verfügbar, die für jede Kombination aus Druck, Feuchte und Temperatur den Dichtewert berechnen.
z. B: http://www.holzfragen.de/seiten/lfe_rechner.html
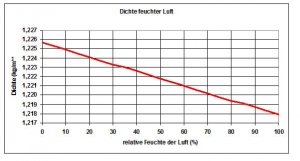
Bezug zur Praxis:
Der Effekt der relativen Luftfeuchte ist im Vergleich zum Temperatureffekt sehr gering. Bei der Thermikbildung dominiert also die Temperatur.
Einfluss der Lufttemperatur auf die Reynoldszahl
Die Bedeutung der Reynoldszahl setze ich als bekannt voraus. Die Re-Zahl ist folgendermaßen definiert:
Re = Fluggeschwindigkeit ⋅ Bezugslänge ⋅ 1/nü
Wobei 1/nü = ρ/μ (1/nü = rho/mü) ist.
μ (mü) ist die Zähigkeit der Luft und nü wird als kinematische Zähigkeit definiert. Wichtig ist dabei: Die Multiplikation von 1/nü mit Länge (Profiltiefe) und Fluggeschwindigkeit ergibt die Re-Zahl.
Die kinematische Zähigkeit hängt von der Temperatur der Luft ab. Die Re-Zahl ändert sich demnach etwas mit der Temperatur.
Für die Kopfrechnung hat sich folgende Formel eingebürgert:
Re= v (m/s) ⋅ Profiltiefe (mm) ⋅ 70
Beispiel: v = 10 m/s, Profiltiefe = 200 mm --> Re = 140 000
Der Wert 70 ist der Wert für 1/nü unter der Berücksichtigung, dass man die Länge in mm und nicht in m einsetzt.
Bei den Standardbedingungen ist nü = 14,4 ⋅ 10–6 m2/s und 1/nü = 69500
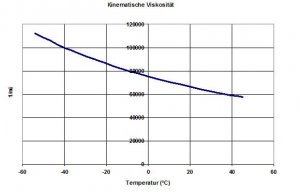
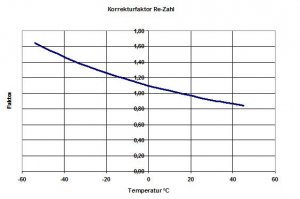
In diesem Diagramm habe ich den Wert für 1/nü bei den Standardwerten auf 1 gesetzt. Man sieht, dass bei tiefen Temperaturen die Re-Zahl höher ist und demzufolge bei höheren Temperaturen als 15°C abnimmt. Diesen Effekt nutzt man in Kryo-Windkanälen aus, um bei höheren Re-Zahlen zu messen. Dabei wird die Luft im Windkanal stark gekühlt.
Wünsche, Kritik und Anregungen nehme ich gerne entgegen: lou.jakob(at)t-online.de
Ein kleiner Ausflug in die Physik unserer Atmosphäre
Wir Modellflieger haben einen ganz besonderen Bezug zu Wind und Wetter. Etwas allgemeiner: Zu der unteren Schicht unserer Atmosphäre, die nicht nur unser Leben sondern auch das Modellfliegen erst ermöglicht.
Die Atmosphäre ist für alle gleich. Die Hummel bewegt sich im gleichen Medium wie ein Airbus solange beide in der gleichen Höhe fliegen. Wenn die Hummel ihre Dienstgipfelhöhe erreicht hat, hat sie etwa die gleichen atmosphärischen Bedingungen wie der Airbus im Landeanflug.
Das Medium Luft will ich im folgenden Aufsatz dem
 -User etwas näher bringen. Die Luftdichte ist z. B. bei Leistungsmessungen an Luftschrauben zu beachten. Die Speedflieger wollen ihre Messungen bei unterschiedlichen Bedingungen diskutieren, usw...
-User etwas näher bringen. Die Luftdichte ist z. B. bei Leistungsmessungen an Luftschrauben zu beachten. Die Speedflieger wollen ihre Messungen bei unterschiedlichen Bedingungen diskutieren, usw...Auftrieb und Widerstand, welche Rolle spielt die Luftdichte?
Da fällt mir doch mein Lieblingsspruch ein:
Beide Kräfte sind direkt proportional zur Luftdichte.
Zur Berechnung dieser Kräfte wurden folgende Gleichungen aufgestellt:
Auftrieb = Staudruck ⋅ Auftriebsbeiwert ⋅ Bezugsfläche
Widerstand = Staudruck ⋅ Widerstandsbeiwert ⋅ Bezugsfläche
Die Bezugsfläche könnte beliebig definiert werden. Bei Flugzeugen hat man sich darauf geeinigt, als Bezugsfläche die Flügelfläche zu nehmen. Die Beiwerte sind dimensionslos und deswegen universell verwendbar. Der Auftriebsbeiwert cA und der Widerstandsbeiwert cW sind bekannte Größen, die wir z. B. aus der Flugzeugpolaren ablesen können.
Für erste Abschätzungen können wir mit cA = 1 und cW = 0,1 arbeiten. Dieses Flugzeug hätte also eine Gleitzahl cA/cW = 10. Je nach Konfiguration können diese Werte sowohl nach oben als auch nach unten überschritten werden.
Der Staudruck ist definiert als:
Staudruck q = 0,5 ⋅ Luftdichte ⋅ Geschwindigkeit ⋅ Geschwindigkeit
Wichtig für uns ist: Die Luftkräfte, also Auftrieb und Widerstand, hängen linear von der Luftdichte und quadratisch von der Geschwindigkeit ab.
Die Dichte der Luft
Jedes Medium, egal ob fest, flüssig oder gasförmig, hat eine Dichte. Sie ist definiert als Masse/Volumen. Gebräuchlich ist z. B. die Masse für 1 m³ (ein Würfel mit 1 m Kantenlänge) eines Stoffs anzugeben.
Wir wissen noch:
1 m3 Wasser hat eine Masse von 1000 kg, also Wasser hat die Dichte (rho) ρWasser = 1000 kg/m3. Die Masse für einen dm3 oder Liter (l) Wasser ist „griffiger“ und damit leichter zu merken. 1 l Wasser hat eine Masse von 1 kg.
Umgangssprachlich dürfen wir auch sagen 1 l Wasser wiegt 1 kg. Genau genommen wiegt 1 l Wasser 9,81 N, das ist die Gewichtskraft, die 1 kg Masse ausübt.
Hier ein paar Werte für andere Stoffe:
Anekdote:
Der kleine Otto wollte die Flugleistung seines Amigo steigern und füllte deswegen seinen folienbespannten Flügel mit Helium. Vom Testflug mit dem Heliumflügel kam er sehr enttäuscht zurück. Er konnte keinen Unterschied feststellen, und eine kleine Rechnung zeigt warum:
Der Flügel hat ein Volumen von ca. 0,003 m3 . Der Auftrieb von 1 m3 Helium beträgt ca. 1,05 kg. Da der Flügel aber nur ein sehr kleines Volumen hat, beträgt der statische Auftrieb auch nur ca. 3 g.
Der Amigoflügel mit Heliumfüllung ist deswegen nur 3 g leichter als ein Flügel mit Luft drin.
Die Dichte der Luft ist nicht konstant, sondern von verschiedenen Parametern abhängig.
Da wir in der Technik für Alles eine Norm erstellen, wurde auch ein Modell der Atmosphäre erstellt. Diese Norm heißt DIN ISO 2533 und beschreibt die sog. „Standardatmosphäre“. Der obige Wert von 1,225 kg/m3 für die Luftdichte ist der Normwert bei einer Temperatur von 15°C und einem Druck von 1013,25 hPa.
Wovon hängt die Luftdichte ab?
Die Dichte der Luft hängt in erster Linie vom Druck und von der Temperatur ab. Später nehmen wir den Einfluss der Luftfeuchte hinzu. Die Verhältnisse werden durch die allgemeine Gasgleichung beschrieben:
(diese Gleichung ist sehr wichtig, und für alle Techniker lohnt es, sich so etwas zu merken!)
Dichte Luft = Druck / (Temperatur ⋅ Gaskonstante)
Wichtig:
Gaskonstante Luft = R = 287,05 J/kg/K
Die Temperatur ist in K einzusetzen wobei gilt:
K = Temperatur in °C + 273,16 also 20°C sind 293,16 K
Beispiel: T = 15°C = 288,16 K; p = 101325 Pa; ρ = 101325/(288,16 ⋅ 287,05) kg/m3 = 1,225 kg/m3Wie stark schwankt der Luftdruck?
Bei der Änderung des Luftdrucks müssen wir zwei Fälle unterscheiden:
- Änderung des Luftdrucks bezogen auf Meereshöhe (NN)
- Änderung des Luftdrucks durch Flughöhe über NN
*Es gibt zwar Gegenden, die unter NN liegen aber praktisch hat das keine Bedeutung.
Der Korrekturterm durch die Höhe wird später erläutert.
Der höchste gemessene Luftdruck in Deutschland betrug 1056,6 hPa. Die höchste gemessene Druckabnahme ca. 100 hPa in 23 h. Der niedrigste Wert liegt bei etwa 856 hPa. Daraus schließen wir, dass sich der Luftdruck um etwa ±5% ändert, und demzufolge sich die Luftdichte durch den Druck auch im gleichen Verhältnis ändert.
Luftdichteänderung durch Temperaturänderung
Wie wir in der allgemeinen Gasgleichung gesehen haben, ist die Luftdichte linear mit der Temperatur verknüpft.
Wichtig: Die Temperatur muss in K eingesetzt werden.
Ich persönlich gehe normalerweise nur bei Temperaturen über 0°C zum Fliegen. Im Sommer oberhalb von 30°C, also bei 303 K wird die Sache sehr schweißtreibend, und es gibt angenehmere Freizeitgestaltungen, z. B. Baden im Bodensee.
Um den Einfluss der Temperatur darzustellen, berechnen wir ein paar Werte für Normaldruck: 101325 Pa.
Betrachten wir den Bereich zwischen -5°C und +30°C stellen wir fest, dass sich in diesem Bereich die Luftdichte um ca. 11,5% ändert.
Abhängigkeit der Dichte von der Flughöhe
Im Modell der Normatmosphäre wird eine Temperaturabnahme von 6,5 K pro 1000 m Höhendifferenz im Bereich zwischen 0 und 11 km Höhe festgelegt. Aus der allgemeinen Gasgleichung und der statischen Grundgleichung der Atmosphäre lässt sich daraus die Änderung der Dichte mit der Höhe beschreiben.
Auswirkung in der Praxis:
Eine Starthöhe von 2000 bis 2500 m ist in den alpinen Fluggebieten durchaus üblich. Eine Startüberhöhung von 500-1000 m je nach Größe des Flugmodells ist möglich (wenn auch nicht immer legal). In dieser Höhe ist die Luftdichte schon deutlich niedriger als am Boden.
Einfluss der Feuchte auf die Dichte
Jeder Student oder Schüler ist schon über die Frage gestolpert: Was ist leichter, trockene oder feuchte Luft?
Die richtige Antwort lautet: Feuchte Luft ist leichter als trockene Luft!
Für uns Modellflieger ist das sehr wichtig. Warme, feuchte Luft steigt nach oben, und wir nutzen diese aufsteigende Luftmasse als Thermik. Wenn feuchte Luft nicht leichter wäre, würden sich keine Wolken bilden.
Die Zusammenhänge sind nicht so trivial. Im Internet sind EXCEL-Programme verfügbar, die für jede Kombination aus Druck, Feuchte und Temperatur den Dichtewert berechnen.
z. B: http://www.holzfragen.de/seiten/lfe_rechner.html
Bezug zur Praxis:
Der Effekt der relativen Luftfeuchte ist im Vergleich zum Temperatureffekt sehr gering. Bei der Thermikbildung dominiert also die Temperatur.
Einfluss der Lufttemperatur auf die Reynoldszahl
Die Bedeutung der Reynoldszahl setze ich als bekannt voraus. Die Re-Zahl ist folgendermaßen definiert:
Re = Fluggeschwindigkeit ⋅ Bezugslänge ⋅ 1/nü
Wobei 1/nü = ρ/μ (1/nü = rho/mü) ist.
μ (mü) ist die Zähigkeit der Luft und nü wird als kinematische Zähigkeit definiert. Wichtig ist dabei: Die Multiplikation von 1/nü mit Länge (Profiltiefe) und Fluggeschwindigkeit ergibt die Re-Zahl.
Die kinematische Zähigkeit hängt von der Temperatur der Luft ab. Die Re-Zahl ändert sich demnach etwas mit der Temperatur.
Für die Kopfrechnung hat sich folgende Formel eingebürgert:
Re= v (m/s) ⋅ Profiltiefe (mm) ⋅ 70
Beispiel: v = 10 m/s, Profiltiefe = 200 mm --> Re = 140 000
Der Wert 70 ist der Wert für 1/nü unter der Berücksichtigung, dass man die Länge in mm und nicht in m einsetzt.
Bei den Standardbedingungen ist nü = 14,4 ⋅ 10–6 m2/s und 1/nü = 69500
In diesem Diagramm habe ich den Wert für 1/nü bei den Standardwerten auf 1 gesetzt. Man sieht, dass bei tiefen Temperaturen die Re-Zahl höher ist und demzufolge bei höheren Temperaturen als 15°C abnimmt. Diesen Effekt nutzt man in Kryo-Windkanälen aus, um bei höheren Re-Zahlen zu messen. Dabei wird die Luft im Windkanal stark gekühlt.
Wünsche, Kritik und Anregungen nehme ich gerne entgegen: lou.jakob(at)t-online.de
Zuletzt bearbeitet von einem Moderator: