Aerodynamikberechnungen
an
Modellflugzeugen
Bedienung und Arbeiten mit FLZ_Vortex
Teil 2 - Auslegungsberechnungen und Feinheiten bei der Panelbelegung (zum Teil 1)
Frank Ranis
an
Modellflugzeugen
Bedienung und Arbeiten mit FLZ_Vortex
Teil 2 - Auslegungsberechnungen und Feinheiten bei der Panelbelegung (zum Teil 1)
Frank Ranis
Dieser Magazinbeitrag ist eine Zusammenfassung des Threads Bedienung und Arbeiten mit FLZ_Vortex
Kapitelübersicht:
- Auslegungsrechnung per Anstellwinkelfunktion
- Auslegungsrechnung per CA
- Auslegungsrechnung per Stabiltätsmaß
- Auslegungsrechnung per Schwerpunkt
- Auslegungsrechnung per Geschwindigkeit
- Fenster 'Berechnete Werte'
- Berücksichtigung zusätzlicher Widerstände
- Luftdichte
- Gesamtpolarenrechnung per Anstellwinkel
- Gesamtpolarenrechnung per Klappenänderung
- Gesamtpolarenrechnung per EWD
- Import von Nurflügel- FLZ- und WinLaengs-Dateien
- Panelauflösung Flügelspitze (Randbogen)
- Panelauflösung an Flügel mit Pfeilungs-Knicken
- Panelauflösung an Flügel mit V-Form
- Panelauflösung in Tiefenrichtung X
1) Auslegungsrechnung per Anstellwinkelfunktion
Bevor wir mit der Rechnung beginnen, noch eine kurze Erläuterung zur Bezeichnung 'Auslegungsrechnung'.
Eine Auslegungsrechnung hat das Ziel, ein Flugzeug für einen bestimmten Einsatzzweck auszulegen.
So kann man sich beispielsweise eine bestimmte Geschwindigkeit als Auslegungsziel vornehmen.
Wir könnten ein Motormodell planen, das mit einer Geschwindigkeit von 60 km/h = 16,667 m/s unterwegs ist. Das Höhenruder (HR) soll dabei 0° Ausschlag haben.
Für alle anderen Geschwindigkeiten muss eine Trimmung durch das HR erfolgen.
Bei Start oder Landung gibt man viel HR, weil das Flugzeug einerseits langsamer als 60 km/h ist und andererseits mehr Auftrieb benötigt.
Andere Auslegungsziele:
Fliegen mit geringstem Sinken (Thermikflug) oder fliegen bei bestem Gleiten (die weiteste Strecke zurücklegen).
Die Auslegung kann auch das Ziel haben, das Modell zunächst für einen Allround-Zustand auszulegen, um dann bestimmte Klappentrimmungen auszurechnen, bei denen z. B. das beste Gleiten oder das kleinste Sinken erreicht wird. Diese Trimmungen kann man gegebenenfalls im Sender speichern und bei Bedarf abrufen.
Für unsere Anstellwinkel-Berechnungs-Versuche laden wir uns das Trainer-File Anhang anzeigen FLZ_Vortex_Anleitung_16.flz herunter.
Wir hatten ja bereits eine Rechnung mit einem Anstellwinkel von 0° gemacht. Unser Ziel war es, die gedachte Rumpf-Bezugslinie im Reiseflug mit 0° zur Anstömrichtung auszurichten, um den Widerstand klein zu halten oder auch, um das Erscheinungsbild der Rumpflage als schön zu empfinden.
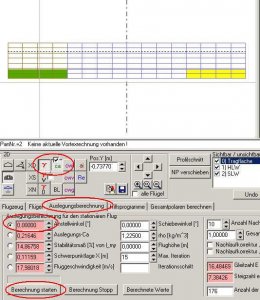
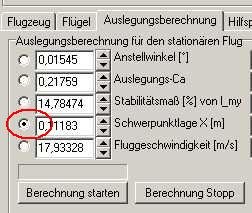
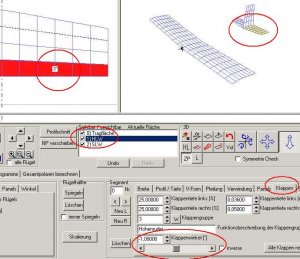
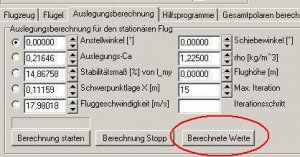
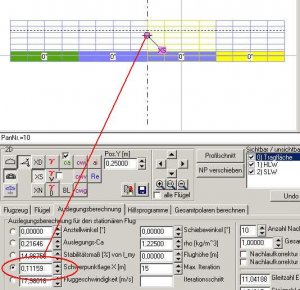
Das Edit-Feld für die Anstellwinkeleingabe finden wir in der Karte 'Auslegungsberechnung'.
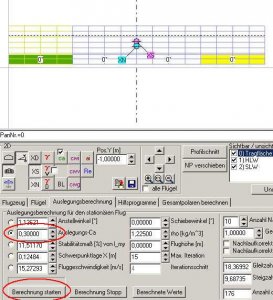
Wir klicken den Radiobutton links neben dem Editdfeld 'Anstellwinkel' an, damit das Programm weiß, welche Funktion es rechnen soll. Zusätzlich aktivieren wir die 2D-Grafik-Schaltbuttons mit dem griechischen Buchstaben Gamma und der Bezeichnung 'ca'.
Bild 81
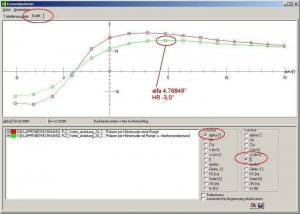
Den Anstellwinkel von 0° lassen wir stehen. Wir rechnen nun einmal, in dem wir auf den Button 'Berechnung starten' links unten klicken.
Nach dem Rechendurchlauf erscheinen in der 2D-Grafik zwei Kurven, eine rote und eine grüne, die leider etwas schlecht zu erkennen ist.
Bild 82
Die rote Kurve zeigt uns die Zirkulationsverteilung (Gamma-Kurve) an und ist im Prinzip wie eine Auftriebs-Kraftverteilung zu verstehen. Für eine richtige Kraft in Newton fehlt diesen Werten aber der Staudruck, die Form der Kurve bleibt aber gleich.
In der Flügelmitte würde eine große Kraft angreifen, die zu den Flügelspitzen hin kleiner wird. Dies wird durch den Druckausgleich an den Flügelspitzen verursacht.
Die zweite, grüne Kurve zeigt die ca-Belastung entlang der Spannweite.
Das Ca (Auftriebsbeiwert) kennt man z. B. auch aus Profilpolaren, dort wird eine Ca-Kurve über der Anstellwinkel-Achse dargestellt. Ab einem bestimmten Anstellwinkel verliert das Profil (hier wäre es ein Profilschnitt entlang der Spannweite) seinen Auftrieb.
Wir machen nun noch weitere Anstellwinkelrechnungen. Dazu tragen wir nacheinander 1°,2°,3° ... 10°,11° in das Edit-Feld 'Anstellwinkel' ein und beginnen jedesmal eine Rechnung mit dem Button 'Berechnung starten'.
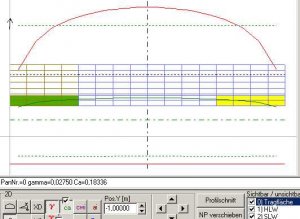
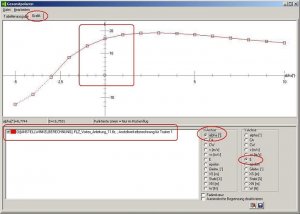
Bitte nach jedem Rechendurchgang die Kurven beobachten! Die Form der Kurven ändern sich in diesem Beispiel nicht, aber es fällt auf, dass die grüne Ca-Kurve je nach Anstellwinkel ein Stück nach oben wandert. Bei einem Winkel von 11° erhalten wir folgendes Bild:
Bild 83
Die rot markieren Bereiche warnen uns vor einem Strömungsabriss. Es macht nun keinen Sinn mehr, mit noch größeren Anstellwinkeln zu rechnen, das entspräche dann nicht mehr der Realität.
Was können wir dieser Rechnung noch entnehmen?
Wir sehen, dass ein Strömungsabriss zuerst in der Flügelmitte stattfindet. Das ist bei einem Rechteckflügel (Trainer, Anfängermodell) typisch und wäre ein gutmütiges Abreißverhalten. Das Modell nimmt dann einfach die Nase runter und holt wieder Fahrt auf, ein Abkippen über eine Fläche wäre nicht zu befürchten. Die Querruder wären weiterhin wirksam. Es gibt aber genug Konstruktionen, bei denen das nicht der Fall ist.
Man schaue sich die berechnete Schwerpunktlage an: 0,152 m. Dies ist nun die absolut hinterste Schwerpunktlage für dieses Modell. Würde ich diese Schwerpunktlage einstellen und dann versuchen, noch Höhe zu ziehen, würde ich noch weiter in der Strömungsabriss geraten. Nur ein Drücken des HRs wäre jetzt noch sinnvoll und hilfreich.
Das Stabilitätsmaß ist mit 2,8% viel zu klein, das Modell reagiert nun heftigst, man kann auch sagen giftig, auf kleinste Störungen oder geringste Klappenausschläge.
Die Einsatzmöglichkeiten einer Anstellwinkel-Rechnung:
Man kann nun...
- ...eine Bezugslinie (z. B. Rumpfachse) gegenüber der Anströmrichtung festhalten und dann die Geometrie ändern, z. B. den Einstellwinkel der Flächen, die Flächengröße und Flächenposition oder auch mit den Klappen spielen, um sein Wunschziel zu erreichen.
- ...schauen, wo ein Strömungsabriss zu erwarten ist.
- ...die hinterste Schwerpunktlage ermitteln.
- ...sich per Hand iterativ an eine Wunschauslegung annähern.
Intern benutzt FLZ_Vortex die Anstellwinkelrechnung, um die anderen Auslegungsfunktionen (CA, Stabimaß, Schwerpunkt, Geschwindigkeit) zu berechnen.
Dazu werden zunächst zwei verschiedene Anstellwinkelrechnungen benutzt, um mittels Sekantenverfahren einen besseren, neuen Anstellwinkel zu ermitteln, der dann näher an der Wunschauslegung liegt. Dies wird mit den jeweils besseren Werten so lange wiederholt, bis sich die gewünschte Genauigkeit einstellt.
[PAGE][/PAGE]
2) Auslegungsrechnung per CA
Der Auslegungsbeiwert CA ist, wie der Name schon sagt, ein Beiwert.
Wichtig ist immer eine Bezugsfläche zum Beiwert zu haben, damit man auch eine Idee hat, wie er entstanden ist.
Das 'A' im 'CA' steht im Deutschen für Auftrieb, im Englischen wird ein 'L' für lift verwendet, daher wird im angelsächsischen Sprachraum ein 'CL' daraus.
Wird der Auftriebsbeiwert groß geschrieben 'CA' oder 'cA', dann ist der Gesamtauftriebsbeiwert z. B. einer Fläche oder eines kompletten Flugzeuges gemeint.
Wird der Auftriebsbeiwert jedoch klein geschrieben, 'ca', dann meint man das ca(y) eines Flügelteilstückes entlang der Spannweite in Y-Richtung.
Das CA entsteht, wenn man die auf eine Oberfläche wirkende Auftriebskraft durch die Oberfläche und den Staudruck teilt. Im Staudruck sind Luftdichte und Geschwindigkeitenthalten. In der Fliegerei wird als Bezugsfläche die auftriebserzeugende Fläche in der Draufsicht (die projezierte Fläche) genommen.
Hier ein paar Links zum CA und zum Staudruck, die ich auf die Schnelle gefunden habe. Speziell die Seite von Hartmut Siegmann (aerodesign) sollte man sich ruhig 20 mal durchlesen.
http://www.aerodesign.de/aero/auftriebsbeiwert.htm
http://de.wikipedia.org/wiki/Auftriebsbeiwert
http://de.wikipedia.org/wiki/Staudruck
http://de.wikipedia.org/wiki/Polardiagramm_(Strömungslehre)
http://wiki.rc-network.de/index.php/Auftriebsbeiwert
In der Anleitung 16 hatten wir bereits die grüne Kurve kennengelernt. Diese besteht aus lokalen Auftriebsbeiwerten ca(y) entlang der Spannweite. Die dazugehörige lokale Bezugsfläche wird immer aus der lokalen Panelbreite und den Flügeltiefen (links und rechts) an diesem Panelstreifen berechnet. Summiert man alle ca(y)*lokale_Bezugsfläche auf und teilt die Summe durch die auftriebserzeugende Fläche des Flügels, kommt man zum Gesamt-CA des Flügels.
Ebenso kann man die Summe der Flügel_CA*Flügel_Auftriebsfläche bilden und durch die gesamtauftriebserzeugende Fläche des Flugzeuges teilen und kommt so zum Gesamt-CA des Flugzeuges.
In der Auslegungskarte finden wir das Eingabefeld für das CA und davor den Radiobutton, um diesen CA-Wert zu fixieren. Dieses CA ist das Gesamt-CA des Flugzeuges.
Die Tabelle (von UweH, aus Thread #98 von Achim) können wir als Grundlage annehmen.
- Speedmodelle: cA 0,10 – 0,25,
- schneller Allrounder: cA 0,35-0,45,
- thermiklastiger Allrounder: ca 0,5-0,6,
- reiner Thermiksegler: ca 0,6-0,7.
Nun laden wir unser Trainermodell FLZ_Vortex_Anleitung_17.flz.
Bild 84
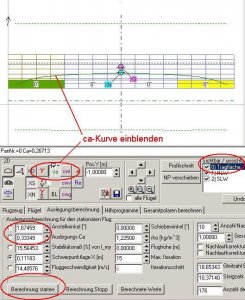
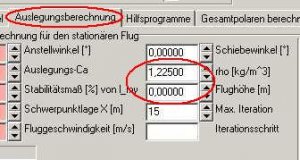
Gehen wir nun in die Auslegungskarte, fixieren die CA-Berechnung mit dem Radiobutton und tragen als CA-Wert CA = 0,3 ein. Anschließend klicken wir auf den Button 'Berechnung starten' und erhalten als Ergebnis das folgende Bild:
Bild 85
Bitte im Kopf behalten: Wir rechnen mit einem stationären Flug, also verläuft die Flugbahn immer schön parallel zum Boden.
Vergleichen wir nun die Werte in beiden Bildern vor und nach der CA-Rechnung.
Der Anstellwinkel hat sich von 0° auf 1,13621° erhöht. Das ist einleuchtend, für etwas mehr Auftrieb (Auftriebsbeiwert von CA = 0,21752 auf CA = 0,3 erhöht) braucht das Flugzeug etwas mehr Anstellwinkel.
Das CA = 0,3 haben wir eingegeben und fixiert, danach wollten wir ja auslegen.
Das Stabimaß hat sich von 14,87% auf 11,51% verringert. Das ist aber doof, ich möchte doch lieber etwa 15% behalten.
Der Schwerpunkt ist von 0,11159 m auf 0,12484 m nach hinten gewandert (also in Richtung Neutralpunkt), daher auch das kleinere Stabimaß!
Die Geschwindigkeit ist kleiner geworden, ist klar, bei mehr Auftrieb für die gleiche stationäre Flugbahn kann ich den Motor drosseln, so dass ich langsamer unterwegs bin.
Was kann ich aber nun gegen die veränderte Schwerpunktlage tun? Ich möchte ja mein Stabimaß von etwa 15% wieder haben.
Machen wir uns mal Gedanken, wie wir auf dem Modellfluggelände die gleiche Fluglage beibehalten, wenn wir die Geschwindigkeit drosseln.
Der Schwerpunkt ändert sich beim realen Modell im Flug nicht (jedenfalls nicht gewollt).
Wir drosseln den Motor und müssen als Ausgleich ein wenig HR ziehen, damit unser Modell durch einen größeren Anstellwinkel mehr Auftrieb bekommt und dann stationär weiter fliegt.
Machen wir das doch hier auch so.
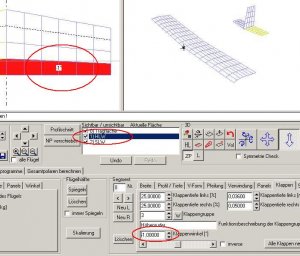
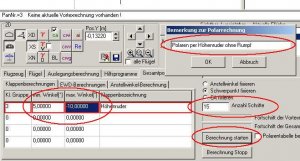
Wir klicken das Höhenleitwerk (HLW) an und gehen in die Unterkarte 'Klappen'. Geben wir mal -1° für den HR-Klappenwinkel ein.
Bild 86
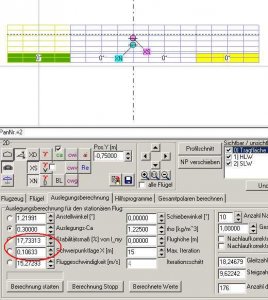
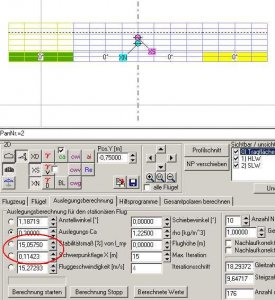
Dann gehen wir zurück in die Auslegungskarte, um eine neue Rechnung mit CA = 0,3 durchzuführen.
Bild 87
WOW, fast ein voller Erfolg! Der Schwerpunkt ist weiter vorne, das Stabimaß ist größer, jetzt allerdings etwas zu groß, wir wollen ja 15%.
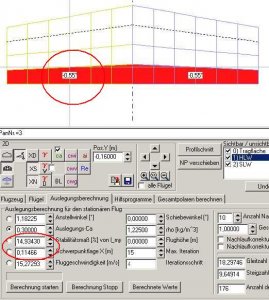
Also erneuts Spiel mit der Klappe, aber mit etwas weniger Ausschlag.
Ich habe das mal gemacht und bin bei einem Klappenausschlag von -0,55° gelandet, um das Stabi auf etwa 15% und damit unseren Schwerpunkt wieder an die alte Stelle zu bekommen.
Bild 88
Ein dauernder Klappenausschlag für unsere CA = 0,3-Auslegung ginge zwar, ist aber nicht so schön. Deshalb möchte ich die Klappe im Auslegungsflug in Neutralstellung haben.
Was kann man als Ersatz für die HR-Klappen-Trimmung nehmen?
Ein Möglichkeit wäre, die Flächengröße des HLWs zu ändern (Anleitung 7). Das ist aber nur schwer zu realisieren, wenn das Modell schon fertig ist. Aber an der EWD lässt sich vielleicht was drehen. Das bedeutet also, die Klappe des HLWs wieder auf 0° einstellen und den Einstellwinkel (Anleitung 10) des HLWs ändern.
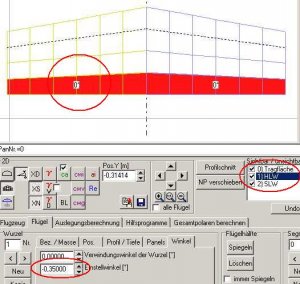
Ich komme damit auf einen Einstellwinkel des HLWs von -0,35°. Das HLW müsste dazu hinten mit einem Stück Balsa (1,2 mm dick) unterlegt werden.
Bild 89
Ergebnis:
Bild 90
Alternativ könnte man auch den Einstellwinkel der Tragfläche ändern oder die EWD auf beide Flächen verteilen, um z. B. die Rumpfbezugslinie wieder auf 0° Anstellwinkel zu bekommen. Das muss man ausprobieren bis es passt.
Was lernen wir noch?
Eine Klappentrimmung (HR, Wölbklappe) kann man auch durch eine Einstellwinkeländerung ersetzen (geänderte EWD). Die EWD ist also im Prinzip eine fest eingebaute Trimmung!
[PAGE][/PAGE]
3) Auslegungsrechnung per Stabiltätsmaß
Das Stabilitätsmaß (kurz Stabimaß oder Stabi) ist ein echt heißes Eisen. Da gibt es die wildesten Diskussionen.
Im Beispiel der Ka6 haben wir schon so eine gewaltige Abweichung gesehen. 15% Stabi wollten wir erst nehmen, 30% Stabi sind es dann geworden. Weiter unten will ich die Probleme mal aufzeigen und zur weiteren Diskussion aufrufen.
Das Stabimaß ist eigentlich der Abstand in Metern [m] zwischen Neutralpunkt und Druckpunkt. Der Druckpunkt ist nachher unser Schwerpunkt, den wir am Modell einstellen. Die Lage von Neutralpunkt und Druckpunkt werden von einem Bezugspunkt (dem Konstruktions-Nullpunkt) aus in [m] angegeben. Somit ist das Stabimaß auch eine Länge in [m].
Weil Längenmaße als Stabi nun schlecht zum Vergleichen von verschiedenen Flugzeugtypen taugen, haben sich die Urgroßväter der Aerodynamik die Geschichte mit der Prozentangabe ausgedacht. Um das Stabimaß in [m] dimensionslos zu machen, verwendet man die Bezugsflügeltiefe l_my, die mittlere aerodynamische Flügeltiefe.
Formel:
Stabimaß[%] = ( Stabimaß[m]/l_my[m]) * 100
Beispiel:
NP ist die Lage des Neutralpunkts, DP die Lage des Druckpunkts (Schwerpunkt), l_my = 0,2 m
Stabimaß[m] = NP - DP = 0,03 m
Stabimaß[%] = (0,03/0,2) * 100 = 15%
Nun kommen wir zur Eingabe und Auslegungsrechnung per Stabimaß. Wir laden dazu wieder unseren Trainer aus [highlight]FLZ_Vortex_Anleitung_11.flz[/highlight].
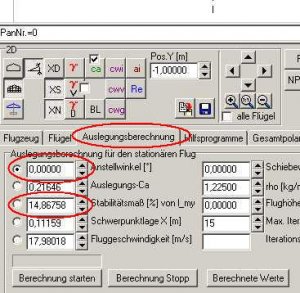
Bei einer Anstellwinkel-Auslegungsrechnung mit 0° hatten wir ein Stabi von 14,86758%
Bild 91
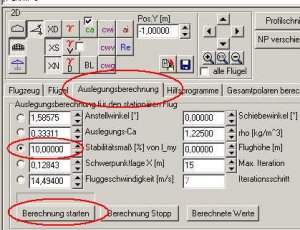
Jetzt gehen wir in die Karte 'Auslegungsberechnung' und fixieren den Radiobutton vor dem Edit-Feld 'Stabilitätsmaß in % von l_my'. Wir tragen in das Editfeld nun 10% ein, gefolgt von einer Berechnung mittels Button 'Berechnung starten'.
Bild 92
Anstellwinkel, CA, Schwerpunkt und Geschwindigkeit haben sich nun verändert, weil der Druckpunkt (durch das Verkleinern des Stabis) näher an den Neutralpunkt gewandert ist.
Wir können nun die Geometriedaten, z. B. Klappenausschläge, Einstellwinkel, Grundriss usw. ändern, um die gewünschten Eigenschaften zu erzielen. FLZ_Vortex wird dann immer versuchen, einen Anstellwinkel zu berechnen, bei dem das Stabimaß 10% beträgt.
Zum Thema Stabilitätsmaß bei Nurflügeln hat Hartmut Siegmann auf seiner Seite http://www.aerodesign.de/nurflugel/swp_nf.htm einiges geschrieben.
Bei Schwanzflugzeugen werden meist Stabimaße von 10% - 15% genommen.
Nun will ich aber zeigen, dass die Prozentangabe beim Stabimaß doch nicht so das Wahre ist.
Ich habe dazu drei Files vorbereitet: Anhang anzeigen Stabi1.flz, Anhang anzeigen Stabi2.flz und Anhang anzeigen Stabi3.flz.
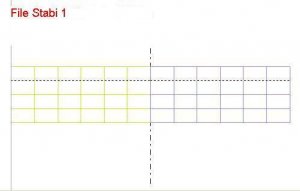
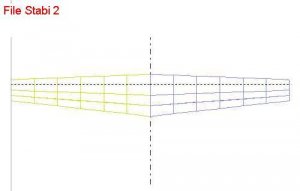
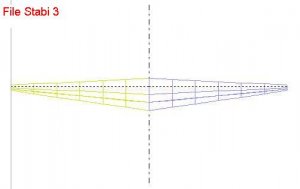
Stabi1 hat einen rechteckigen Tragflügelgrundriss, in Stabi2 ist die Tragfläche mäßig zugespitzt und Stabi3 hat eine große Zuspitzung.
Die Flächeninhalte von Tragfläche und HLW sind in allen Files identisch.
Tragfläche: 0,45 m²,
HLW: 0,06 m²
Bild 93
Bild 94
Bild 95
Bei allen drei Files habe ich eine Auslegungsrechnung per Schwerpunkt gemacht und zwar Druckpunkt = Schwerpunkt = 0,1 m.
Dann habe ich durch minimales Verschieben des HLWs in X-Richtung sowie durch eine leichte Anpassung des Einstellwinkels beim HLW bei jedem File ein CA von 0,2 und einen Neutralpunkt bei 0,14 m eingestellt.
Wie ich oben schon sagte, ist das Stabimaß der Abstand zwischen Neutralpunkt und Druckpunkt (Schwerpunkt) und wird zunächst in [m] gemessen und erst dann in [%] von l_my umgerechnet.
Folgende Daten sind bei allen drei Modellen identisch:
CA = 0,2
Druckpunkt = Schwerpunkt = 0,1 m
Neutralpunkt = 0,14 m
Stabimaß in m = 0,04 m
Jetzt aber die Wahrheit des Stabimaßes in [%].
Flieger Stabi1.flz Stabimaß[%] = 13,45419%
Flieger Stabi2.flz Stabimaß[%] = 17,20637%
Flieger Stabi3.flz Stabimaß[%] = 19,56920%
Obwohl alle drei Modelle ein metrisches Stabimaß von 0,04 m haben (also gleiche Stabilität), gibt es große Differenzen beim Stabimaß in [%].
Das liegt einzig und allein an der Bezugsflügeltiefe (l_my), die durch die Zuspitzung der Tragflächen stark unterschiedlich ist.
Modell Stabi1.flz hat ein l_my von 0,29734 m
Modell Stabi2.flz hat ein l_my von 0,23246 m
Modell Stabi3.flz hat ein l_my von 0,20440 m
Das ist also der Grund, warum die Ka6 so aus dem Rahmen fällt: Wegen der starken Zuspitzung der Tragfläche. Bei den teilweise extrem zugespitzten Nurflügeln á la Horten tritt das gleiche Problem auf. Je nach Grundriss sind dann 15%, 20% oder 25% Stabimaß [%] notwendig.
Wer eine andere Normierung für das Stabimaß findet, kann sich bestimmt Lorbeeren verdienen. Oder auch eine Schelle, weil sich das mit den [%] so in den Hirnen eingebrannt hat.
Nebenbei, wenn hier jemand über das l_my meckern will, im FLZ_Vortex wird dieser Wert, aus allen vorhandenen Flügeln gemittelt, berechnet. Er weicht also vom l_my der größten Tragfläche etwas ab.
[PAGE][/PAGE]
4) Auslegungsrechnung per Schwerpunkt
Wenn es um Berechnungen mit Klappen geht, dann sollte man den Schwerpunkt festhalten (fixieren). Dies ist ja beim realen Modell auch der Fall. Der Schwerpunkt ändert sich im Flug in der Regel nicht, es sei denn
1) ein Bauteil löst oder verschiebt sich
2) oder man hat den Tank ungünstig eingebaut, so dass sich bei leerem Tank das Massenzentrum verschiebt
Wir laden wieder unseren Trainer FLZ_Vortex_Anleitung_19.flz.
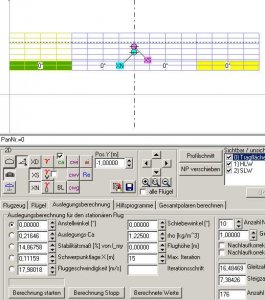
Nun fixieren wir das Edit-Feld 'Schwerpunktlage X[m]' mit dem Radiobutton vor diesem Eingabefeld.
Bild 96
Eine Anwendung wäre z. B. die Berechnung der Minimalgeschwindigkeit für unser Trainermodell.
Dazu verwenden wir das HR und verstellen dieses in kleinen Schritten auf Höhe (negativer Ausschlag, HR geht nach oben).
Erst einen Doppelklick auf das HLW in der 3D-Grafik, dann in den Kasten 'Segmente' und dort in die Unterkarte 'Klappen' wechseln. Hier geben wir zunächst einen HR-Klappenwinkel von -1° in das Edit-Feld 'Klappenwinkel' ein oder verwenden den Schieber.
Bild 97
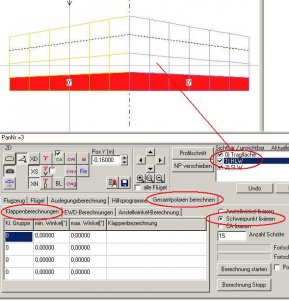
Dann gehen wir zurück in die Karte 'Auslegungsrechnung', wieder die Tragfläche anwählen und den Button 'Berechnung starten' drücken.
Bild 98
Wir sehen nun, dass mit dem Höhe geben das CA und der Anstellwinkel größer werden, es wird also mehr Auftrieb erzeugt.
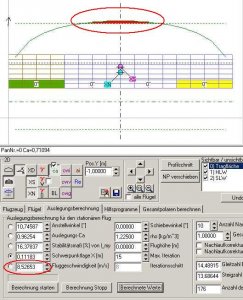
Das Spiel mit der Klappe (immer -1° mehr) und dem Berechnen wiederholen wir solange, bis sich folgendes Bild ergibt:
Bild 99
Bei einem HR-Ausschlag von etwa -7° zeigen sich erste Anzeichen eines Strömungsabrisses an der Tragfläche. Würden wir noch weiter HR ziehen, dann wären noch größere Bereiche der Tragfläche vom Abriss betroffen.
Wir wollten die Minimalgeschwindigkeit berechnen, bei der sich unser Modell gerade noch so auf einer stationären Flugbahn (parallel zum Boden) halten kann. Diese Geschwindigkeit können wir im unteren Edit-Feld 'Fluggeschwindigkeit [m/s]' ablesen. Die Minimalgeschwindigkeit liegt also bei etwa 8,5 m/s oder 30,6 km/h.
Interessant ist noch, wie die ca-Verteilung an unserem HLW aussieht und ob dieses auch von einem Abriss betroffen ist. Dazu wählen wir das HLW aus und schauen uns dort die ca-Kurve an.
Bild 100
Wir erkennen, dass zwischen der durchgezogenen ca-Kurve (grün) und der Strichpunktlinie (Linie des Strömungsabrisses) noch reichlich Luft ist. Das HLW arbeitet also in einer gesunden Strömung und es droht hier keine Gefahr.
[PAGE][/PAGE]
5) Auslegungsrechnung per Geschwindigkeit
Ab und zu kommt es vor, dass wir unser Flugzeug für eine bestimmte Geschwindigkeit auslegen möchten. Pylon- und Speedflieger brauchen so etwas schon mal.
Wir laden das File FLZ_Vortex_Anleitung_20.flz.
In der Karte 'Auslegungsberechnung' klicken wir den Radiobutton vor dem Edit-Feld 'Fluggeschwindigkeit [m/s]' an.
Die Fluggeschwindigkeit wird im FLZ_Vortex in m/s angegeben. Ein Umrechnung auf km/h ist aber total simpel. Hierzu wird einfach der Faktor 3,6 benutzt.
Beispiel:
Als Vorgabe möchten wir 100 km/h haben.
100 km/h / 3.6 = 27,77778 m/s.
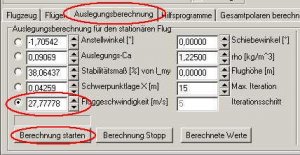
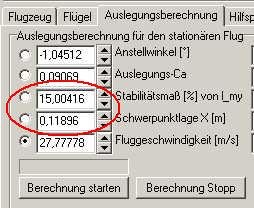
Im Vortex geben wir 27,77778 m/s in das Editfeld für die Fluggeschwindigkeit ein und klicken auf den Button 'Berechnung starten'. Heraus kommt das:
Bild 101
Wir sehen, dass der Anstellwinkel kleiner wurde, er beträgt nun -1,7°. Auch das CA ist kleiner geworden und steht bei 0,091.
Das Stabimaß ist größer geworden. Statt 15% haben wir nun 38%! Etwas zu viel, das müssen wir wieder runter bekommen. Dem entsprechend hat sich auch der Schwerpunkt nach vorne bewegt, ist also weiter weg von unserem Neutralpunkt. Die Geschwindigkeit von 27,77778 m/s = 100 km/h entspricht unserer gewollten Auslegung.
Versuchen wir nun, das Stabimaß wieder auf 15% zu bekommen. Dazu stehen mehrere Möglickeiten zur Wahl:
- Die Fläche des HLWs verkleinern.
- Den Hebelarm zum HLW verkleinern (Abstand Tragfläche->HLW).Diese beiden Möglichkeiten scheiden bei einem fertigen Modell allerdings aus.
- Höhenruder auf tief stellen (positiver Ausschlag, also nach unten).
Das wäre beim realen Flug die Situation, wir geben Gas und müssen etwas Tiefe trimmen, um die stationäre Flugbahn zu halten. Wir möchten aber generell unser Modell auf diese Geschwindigkeit auslegen, um ohne Klappentrimmung auszukommen.
Wir hatten gelernt:
Eine Klappentrimmung (HR, Wölbklappe) kann man durch eine Einstellwinkeländerung ersetzen (geänderte EWD).
4) Eine Einstellwinkeländerung, z. B. an der Tragfläche.
Wir unterlegen unsere Tragfläche an der Endleiste mit einem Streifen Balsa.
Der Einstellwinkel der Tragfläche wird dadurch kleiner (Hintern hoch).
(Anm. d. Redaktion: Beim Hoch- oder Schulterdecker ist das anders als beim Tiefdecker!)
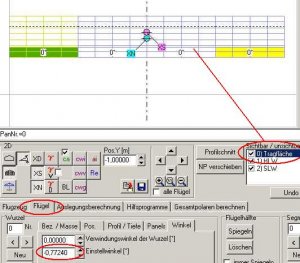
Für ein Stabimaß von 15% bei einer Flugeschwindigkeit von 27,77778 m/s benötigen wir einen Einstellwinkel der Tragfläche von -0,77240°.
Das habe ich einfach ausprobiert. Einstellwinkel ändern, rechnen und ändern, rechnen und ändern, rechnen... usw.
Bild 102
Flugs den Windows-Taschenrechner raus und mit der SIN-Funktion den Einstellwinkel in Balsadicke umrechnen.
(Anm. d. Redaktion: Eine Alternative ist das EWD-Tool aus dem
 -MAGAZIN, da ist diese Berechnung enthalten [heißt dort: Variation der EWD!])
-MAGAZIN, da ist diese Berechnung enthalten [heißt dort: Variation der EWD!])Formel:
SIN(Winkel) = Gegenkathete/Hypotenuse
Die Hypotenuse ist unsere Flügeltiefe = 300 mm,
die Gegenkathete = Balsadicke brauchen wir,
den Winkel = Einstellwinkel = -0,77240° kennen wir, diesen nehmen wir aber positiv, weil sonst die Balsadicke negativ wird.
Umgestellt zur Gegenkathete = Balsadicke:
Balsadicke[mm] = SIN(0,77240°) * 300 mm = 4,04415445 mm, also rund 4 mm.
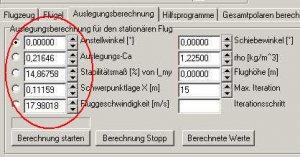
Nach der Einstellwinkeländerung und einer neuen Rechnung sehen die Werte nun so aus:
Bild 103
Als EWD haben wir anstelle von 0° jetzt -0,77240° .
Es muss also nicht immer heißen: EWD = 1,5°, passt schon!
Es kommt auf die Auslegung an.
[PAGE][/PAGE]
6) Fenster 'Berechnete Werte'
Wir laden das File FLZ_Vortex_Anleitung_21.flz.
Dann führen wir eine Auslegungsberechnung per Anstellwinkelfunktion mit 0° Anstellwinkel durch.
Bis jetzt haben wir nach einer Auslegungsrechnung nur wenige Ergebniswerte betrachtet. Folgende Werte können wir direkt der Karte 'Auslegungsberechnung' entnehmen:
Den Auftriebsbeiwert CA,
das Stabilitätsmaß[% von l_my],
den Schwerpunkt [m] sowie
die Geschwindigkeit [m/s].
Bild 104
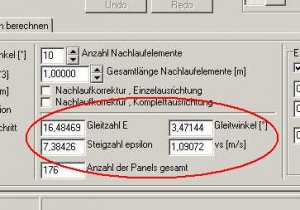
In der Karte 'Auslegungsberechnung', Mitte unten, sehen wir weiterhin:
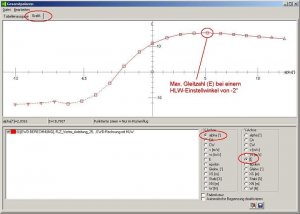
Die Gleitzahl E,
den Gleitwinkel [°],
die Steigzahl (Epsilon),
sowie die Sinkgeschwindigkeit vs [m/s].
Bild 105
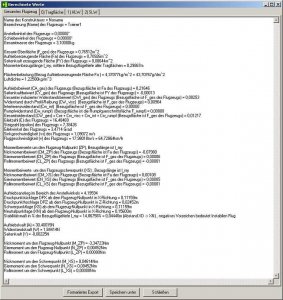
Liegt uns eine gültige Auslegungsrechnung vor, so können wir rund um unser Flugzeug weitere berechnete Werte abrufen. Dazu betätigen wir den Button 'Berechnete Werte'.
Bild 106
Nun erscheint ein neues Fenster.
Bild 107
Oben können verschiedene Karten angewählt werden. Die erste Karte beinhaltet Ergebniswerte für das gesamte Flugzeug. Die bereits bekannten Daten aus der Karte 'Auslegungsberechnung' sind auch hier wieder zu finden.
Je nach Anzahl von Flügeln stehen weitere Karten mit Daten bereit, die dann nur die einzelnen Flügel betreffen. In der Kartenüberschrift findet man die Nummer des Flügels und dessen Bezeichnung (z. B. 0 Tragflügel, 1 HLW usw.).
Ein großer Teil der Daten wird durch den Text erklärt.
[PAGE][/PAGE]
7) Berücksichtigung zusätzlicher Widerstände
Durch den Druckausgleich an den Flügelenden werden Randwirbel erzeugt. Diese beeinflussen die Auftriebsverteilung entlang der Flügelspannweite, so dass zum Flügelende hin immer weniger Auftrieb zur Verfügung steht. Dieser Auftrieb muss ja irgendwo bleiben, es entsteht der sogenannte „induzierte Widerstand“.
Ein weiterer Widerstand wird durch die Reibung auf der Profiloberfläche in der Grenzschicht verursacht. Der vordere Teil der Grenzschicht ist zunächst laminar (parallele Stromlinien). Diese laminare Grenzschicht schlägt dann in eine turbulente Grenzschicht um. Im Übergangsbereich zwischen laminar und turbulent entsteht meist eine Blase, die viel Widerstand verursacht.
Dann gibt es noch den Interferenzwiderstand, der im Übergangsbereich verschiedener Bauteile, z. B. vom Rumpf zum Flügel entsteht.
Schließlich gibt es noch den Rumpfwiderstand.
Alle Widerstände zusammengefasst:
- Induzierter Widerstand, wird durch die Auftriebsverteilungsrechnung des Vortex-Lattice berücksichtigt,
- Profilwiderstand, wird am Schluss nach einer Auftriebsverteilungsrechnung auch vom Programm automatisch berechnet,
- Blasenwiderstand, dieser lässt sich manuell abschalten, wenn z. B. ein Turbulator Verwendung findet,
- Interferenzwiderstand, diesen können wir aus einer Liste auswählen,
- Rumpfwiderstand, hierzu wird die Querschnittsfläche des Rumpfs benötigt und zusätzlich eine Angabe zur Rumpfform aus einer Liste.
Hier soll es nun um die Eingabe der letzten drei Komponenten gehen.
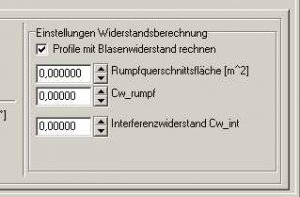
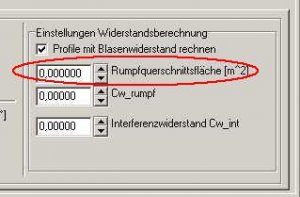
Die Eingabefelder für die zusätzlichen Widerstände finden wir in der Karte 'Auslegungsberechnug' ganz rechts.
Bild 108
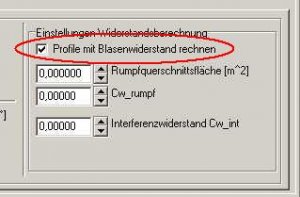
Wir sehen hier die Checkbox mit der Bezeichnung 'Profile mit Blasenwiderstand rechnen'.
Benutzen wir keinen Turbulator, dann sollte diese Checkbox ein Häkchen beinhalten, das heißt, der Blasenwiderstand wird mit berechnet. Hat man einen Turbulator aufgeklebt, dann ist diese Checkbox leer.
Bild 109
Rumpfquerschnittfläche:
Dazu nehmen wir die größte Querschnittsfläche, die wir in der Frontansicht des Rumpfs sehen können.
Übertreibt es dabei aber nicht, zwar sollte man so gut wie möglich rechnen, aber nicht auf ein 1000stel genau!
Bei einem Rechteckrumpf ist die Sache einfach:
Querschnittsfläche [m²] = Höhe[m] * Breite [m].
Eine Kreisfläche berechnet man wie folgt:
Querschnittsfläche [m²] = D[m]²* PI/4 oder
Querschnittsfläche [m²] = r[m]² * PI
mit
D = Durchmesser
r = Radius
Einen elliptischen Rumpf berechnen:
Querschnittsfläche [m²] = D1[m] * D2[m] * PI/4 oder
Querschnittsfläche [m²] = r1[m] * r2[m] * PI
D1, D2 = Druchmesser1, Durchmesser 2
r1, r2 = Radius1, Radius2
Achtung: Maße in m
Die berechnete Querschnittsfläche tragen wir in das Editfeld 'Rumpfquerschnittfläche [m^2]' ein.
Bild 110
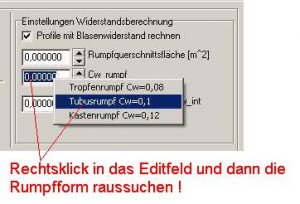
Rumpf-CW:
Kennen wir den Rumpf-CW, dann tragen wird diesen in das Feld 'CW_Rumpf' ein. In der Regel kennt man diesen Wert aber nicht, dann müssen wir ein CW aus der Tabelle entnehmen. Dazu machen wir einen Rechtsklick in das Edit-Feld für die CW-Rumpfeingabe und suchen uns einen passenden Rumpf aus.
Bild 111
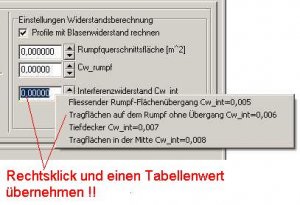
Interferenz-Widerstand:
An Rumpf-Flächenübergängen entstehen Wirbel, die zusätzlichen Widerstand verursachen. Diesen Widerstand tragen wir in das Editfeld 'Inteferenzwiderstand CW_int' ein. Kennen wir den Widerstand nicht, können wir auch hier wieder einen Tabellenwert nehmen. Rechtsklick in das passende Editfeld und einen Tabelleneintrag wählen.
Bild 112
Das CW für den Rumpf scheint auf den ersten Blick gewaltig groß zu sein. Der Grund ist die Bezugsfläche für diesen Wert. Der Rumpf-CW ist auf die Querschnittsfläche bezogen, während alle anderen CWs auf die Flügeloberflächen bezogen sind. Im FLZ_Vortex wird das umgerechnet.
Rechnen wir ohne die zusätzlichen Widerstände, kommen oft traumhafte Werte für Gleitzahl und Sinkgeschwindigkeit heraus.
Wer also beeindrucken (oder sich in die Tasche lügen) will, der lässt die zusätzlichen Widerstände einfach weg.
[PAGE][/PAGE]
8) Luftdichte
Geht es um die tatsächlichen Kräfte (Auftrieb, Widerstand) in Newton [N] oder die Momente [Nm] rund um unser Flugzeug, dann spielt die Luftdichte eine wichtige Rolle.
Wir müssen den Auftrieb in Newton kennen, um unsere Flugzeugmasse [kg] in der Luft zu halten. Den Widerstand in Newton brauchen wir, um genau den Antrieb auswählen zu können, der eine konstante Geschwindigkeit oder sogar eine Beschleunigung möglich macht (Schubkraft).
Die Luftdichte wird in kg/m³ gemessen und beträgt auf der Erdoberfläche in etwa 1,225 kg/m³.
Der Auftrieb in [N] wird mit folgender Formel berechnet.
Auftrieb in N:
A = CA * q * F
A = Auftrieb (N)
q = Staudruck (Pa)
F = Bezugsfläche (m²)
CA = Auftriebsbeiwert
Der Staudruck wird mit Hilfe der Geschwindigkeit und der 'Luftdichte' berechnet.
Staudruck (Geschwindigkeitsdruck):
q = p*U~²/2
p = Dichte (kg/m³) 1.225 in Höhe 0
U~ = ungestörte Anströmgeschwindigkeit in m/s
Mit zunehmender Höhe nimmt die Luftdichte ab, die Luft wird also dünner, so dass wir an folgenden Parametern „schrauben“ können, um den Auftrieb wieder hinzubekommen.
- Geschwindigkeit erhöhen, der Antrieb muss das natürlich schaffen.
- CA (sprich Anstellwinkel) erhöhen, hier gibt es aber die Grenze CA-max.
- Die auftriebserzeugende Oberfläche vergrößern.
In älteren Version <1.190 vom FLZ_Vortex konnte man die Luftdichte nur indirekt über die Eingabe der Flughöhe (Karte Auslegungsberechnung) beeinflussen. Ab V1.190 kann man die Luftdichte direkt eingeben, Eingabefeld roh [kg/m^3].
Bild 113
Intern wird die Luftdichte nach einer Tabelle umgerechnet. Siehe hierzu auch Kapitel, 14.8: Flughöhe, in der Hilfe von FLZ_Vortex.
Für unseren Zweck, die Auslegung von Flugzeugen, reicht es völlig aus, wenn wir die Flughöhe auswählen.
Möchten wir aber Messungen (mit einem Daten-Logger) machen, dann sollte man die Luftdichte etwas genauer eintragen, um Vergleiche zwischen Theorie und Praxis anstellen zu können.
Hierzu hat Florian Rösch ein Skript geschrieben, Danke Florian.
Anhang anzeigen Memo Auswertung Messfluege.pdf
Florian hat hier Formeln hinterlegt, mit denen es möglich ist, auch die Temperatur und den Luftdruck zu berücksichtigen, was dann alles sehr viel genauer macht.
[PAGE][/PAGE]
9) Gesamtpolarenrechnung per Anstellwinkel
Bei den bisherigen Berechnungen haben wir immer nur einen Auslegungszustand berechnet.
In der Karte 'Gesamtpolaren berechnen' hat man aber die Möglichkeit, eine Folge von Berechnungen mittels einer Schleife durchzuführen.
Es wird ein Start- und Endwert, sowie die gewünschte Anzahl von Schritten vorgegeben und das Programm berechnet dann automatisch eine Folge, die in einer Tabelle abgelegt wird. Mit Hilfe einer Grafik kann man sich anschließend die Polaren anschauen und hat somit einen besseren Überblick, um sein Modell einstellen zu können.
In FLZ_Vortex gibt es drei unterschiedliche Möglichkeiten für die Gesamt-Polarenberechnung.
- Klappenberechnung,
- EWD-Berechnung und
- Anstellwinkelberechnung
In dieser Anleitung soll es um die Anstellwinkelberechnung gehen.
Wir laden das Demomodell FLZ_Vortex_Anleitung_24.flz.
Die Anstellwinkel-Berechnung kann man nutzen, um einen ersten Überblick bezüglich Gleit- und Steigzahl zu bekommen oder um zu schauen, wo ein halbwegs günstiger Schwerpunktsbereich mit den aktuellen EWD- oder Klappeneinstellungen zu finden ist.
EWD und Klappen werden in der Gesamtpolaren-Anstellwinkelberechnung nicht verändert, bleiben also so, wie sie zuletzt eingestellt wurden.
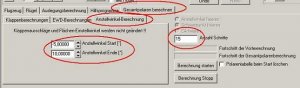
Nachdem wir das Modell geladen haben, gehen wir in die Karte 'Gesamtpolaren berechnen' und in die Unterkarte 'Anstellwinkelberechnung'. Hier tragen wir in das Editfeld 'Anstellwinkel Start' -5° und in das Editfeld 'Anstellwinkel Ende' 10° ein. Es sollen also Anstellwinkel-Berechnungen von -5° bis +10° durchgeführt werden.
Des Weiteren braucht das Programm noch eine Angabe, wie viele Berechnungen durchgeführt werden sollen, das ist quasi die Auflösung der Polarentabelle.
Wir tragen in das Editfeld 'Anzahl Schritte' eine 15 ein, ist ja nur ein Beispiel.
Zwischen -5° und +10° ergibt sich so eine Schleife mit 15 Zwischenschritten (-5°, -4°, -3° ..... bis +10°), das ergibt dann 16 Tabelleneinträge.
Bild 114
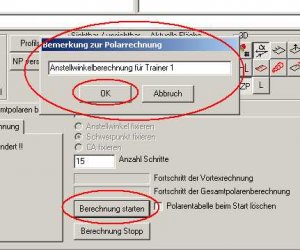
Wenn wir mit den Eingaben fertig sind, klicken wir auf den Button 'Berechnung starten'.
Darauf hin öffnet sich ein Fester mit einem Textfeld, in das wir eine Bemerkung zu der folgenden Berechnung eintragen können. Der Text ist beliebig und soll nur eine Info sein, damit wir den Überblick behalten, wenn es verschiedene Polaren in der Tabelle oder Grafik gibt.
Nach einer Bestätigung (Button OK) der Infoeingabe geht es mit den Berechnungen los.
Bild 115
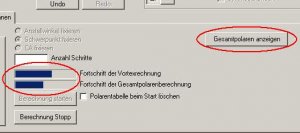
Es dauert nun eine Weile, bis das Programm alle Anstellwinkel gerechnet hat. Am Fortschrittsbalken...
Bild 116
...kann man erkennen, wie lange es noch dauert. Ist das Programm fertig, betätigen wir den Button 'Gesamtpolaren anzeigen'. Daraufhin öffnet sich ein neues Fenster.
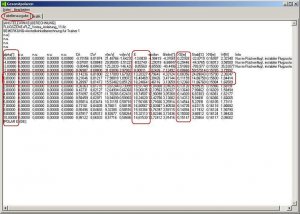
Bild 117
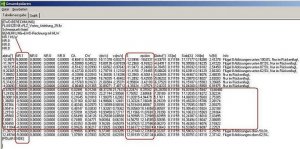
Hier sehen wir zunächst die Tabelle, die FLZ_Vortex eben berechnet hat. Man könnte sich nun z. B. für die Gleitzahlen E interessieren, ich habe das oben mal markiert.
Im Anstellwinkelbereich von -1° bis +1° ergeben sich die Gleitzahlen 13,2 , 16,5 und 18,25.
Ich habe diesen Bereich ausgewählt, weil hier das Stabimaß im gutmütigen Bereich liegt, also etwa zwischen 12% und 25%. Der einstellbare Schwerpunktbereich XS [m] liegt dann zwischen 0,084 m und 0,124 m.
Bei allen anderen Anstellwinkeln würde das Stabimaß entweder sehr groß oder zu klein werden.
Man kann sich die berechnete Tabelle auch als Grafik anschauen. Dazu wählen wir die Karte 'Grafik'.
Bild 118
Links unten kann man die Polarentabellen auswählen. Hier gibt es allerdings nur eine, es könnten aber auch mehrere sein.
Rechts wählt man einen Radiobutton für die X-Achse und einen für die Y-Achse aus, hier mal Anstellwinkel (X-Achse) und Gleitzahl E (Y-Achse).
Den Anstellwinkelbereich -1° bis +1° habe ich markiert.
Die beste Gleitzahl (~ 19) würde sich bei einem Anstellwinkel um 3° ergeben, aber dann wäre das Stabimaß zu klein (siehe Tabelle).
Die berechneten Polaren lassen sich auch auf Festplatte speichern oder bereits vorhandene Polaren als Vergleich dazu laden.
Bild 119
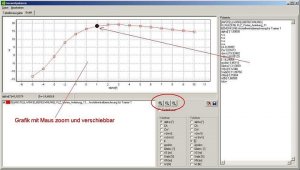
Die hier dargestellte Grafik ist der Stand bis Software-Version v1.90. Ab v1.91 habe ich eine neue Grafikausgabe gebastelt.
Bild 120
In dieser Version kann man die Grafik zoomen und verschieben. Des Weiteren gibt es die Möglichkeit, sich einen Punkt zu markieren, dessen Polareninfos dann rechts eingeblendet werden.
[PAGE][/PAGE]
10) Gesamtpolarenrechnung per Klappenänderung
Bei der Gesamtpolarenrechnung per Anstellwinkel wurde das Modell einfach durch eine Folge von Anstellwinkeln gefahren. Mit jedem Anstellwinkel änderte sich der Druckpunkt und somit die Lage des Schwerpunkts.
Haben wir aber einen fixen Schwerpunkt, so wie es nachher in der Realität beim echten Flugzeug der Fall ist, muss man die Lage des Flugzeugs per Klappenausschlag einstellen.
Möchten wir untersuchen, wie das Modell auf Klappenausschläge reagiert, dann benutzen wir die Gesamtpolaren-Klappenrechnung.
Ich habe unseren Trainer aus Anleitung 11 etwas modifiziert und zusätzlich eine Wölbklappe eingebaut, die wir später benutzen wollen.
Anhang anzeigen FLZ_Vortex_Anleitung_25.flz
Im Folgenden denken wir uns den Trainer mal als Segelflugzeug ohne Antrieb.
Wir laden dieses FLZ_File und gehen in die Karte 'Gesamtpolaren berechnen' und dortin die Unterkarte 'Klappenberechnung'. Zusätzlich wählen wir das HLW als aktiv an, da wir im Folgenden eine Polarenrechnung über HR machen möchten.
Bild 121
Des Weiteren wird der Radiobutton 'Schwerpunkt fixieren' eingeschaltet, da wir ja auch später mit fester Schwerpunktlage fliegen werden. Es wird also der aktuell vorhandene Schwerpunkt genommen, der in der Karte 'Auslegungsberechnungen' steht.
Bild 122
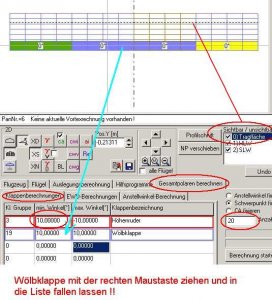
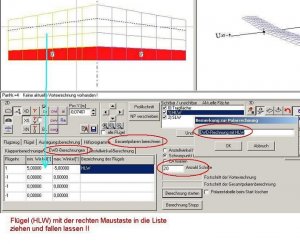
Links unten in der Karte 'Klappenberechnung' sehen wir ein Liste, in die wir vier verschiedene Klappenguppen eintragen können. Kennen wir die Gruppennummer unseres HRs, so tragen wir die Nummer unter 'Klappengruppe' ein.
Die Klappengruppe für das HR ist in diesem Fall die Nr. 3. Alternativ kann man das HR in der 2D-Grafik mit der rechten Maustaste anklicken und bei gedrückter Maustaste unten in die Liste ziehen (drag and drop).
Hat alles geklappt, sieht es wie folgt aus:
Bild 123
In die drei anderen Listenzeilen könnte man nun noch weitere Klappengruppen eintragen, wir beschränken uns erst mal auf das HR.
Im nächsten Schritt müssen wir festlegen, welcher Klappenwinkelbereich berechnet werden soll.
Wir entscheiden uns für den Bereich +5° bis -10°.
Diese Eckwerte tragen wir in die Liste unter 'min. Winkel' und 'max. Winkel' ein. Für die Anzahl Schritte wählen wir '15' und starten die Berechnung. Als Info tragen wir ein 'Polaren per HR ohne Rumpf', denn gleich wollen wir noch den Widerstand des Rumpfs mit einbeziehen, was wir bis jetzt noch nicht gemacht haben.
Bild 124
Bevor wir uns die Polaren anschauen, machen wir noch eine Rechnung mit den zusätzlichen Widerständen.
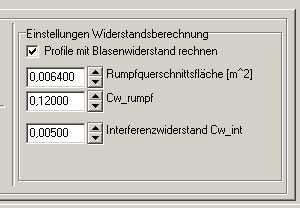
Dazu gehen wir in die Karte 'Auslegungsberechnung' und tragen rechts unter 'Einstellungen Widerstandsberechnung' folgende Werte ein:
- Rumpfquerschnitt (80 mm*80 mm) = 0,0064 m^2
- CW-Rumpf (Kastenrumpf) = 0,12000
- Interferenzwiderstand = 0,00500
Bild 125
Nun gehen wir zurück in die Gesamtpolarenrechnung und machen einen Neustart mit der Info 'Polaren per HR mit Rumpf- u. Interferenzwiderstand'.
Ist das Programm fertig, betätigen wir den Button 'Gesamtpolaren anzeigen'.
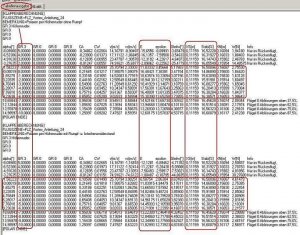
Zunächst die Tabelle:
Bild 126
Hier finden wir unsere zwei Polaren wieder.
Oben die Polare ohne zusätzliche Widerstände (Rumpf und Interferenz).
Unten die Polare mit zusätzlichen Widerständen.
Die Spalte an zweiter Stelle (GR.3) zeigt die Höheruderausschläge. Interessant sind hier nur die Klappenauschläge von +1° bis -6°.
Bei allen anderen Ausschlägen müssten wir entweder im Rückenflug unterwegs sein oder der Flügel hat größere Bereiche mit einem Strömungsabriss.
Bei den Spalten Schwerpunkt (XS) und Stabi sehen wir recht konstante Werte, weil wir ja unseren Schwerpunkt bei der Berechnung fixiert haben.
Für die Segelflugeigenschaften sind die Spalten Gleitzahl (E für Streckenflug) und Steigzahl (epsilon für Thermikflug) interessant. Dort gibt es zwischen der oberen und unteren Tabelle deutliche Unterschiede. In der oberen Tabelle (ohne Zusatzwiderstand) liegt die max. Gleitzahl (E) bei 18,9, in der unteren Tabelle (mit Zusatzwiderstand) bei etwa 15. Die größte Steigzahl oben bei 13,8 und unten bei 12,2.
Wir erkennen weiterhin, dass wir für das beste Gleiten (Gleitzahl E) und das kleinste Sinken (vs) bzw. das beste Steigen (epsilon) unterschiedliche Höhenruderstellungen brauchen.
Für das Gleiten (untere Tabelle) müssten wir einen HR-Ausschlag von -3° wählen und für den Thermikflug einen Klappenausschlag von -6°.
Gehen wir nun in die Grafik.
Gleitzahl:
Bild 127
Wir wählen für die X-Achse den Radiobutton 'Alfa' und für die Y-Achse 'E' für Gleitzahl.
Man sieht deutlich den Unterschied zwischen der Rechnung ohne Zusatzwiderstände (rot) und mit zusätzlichen Widerständen (grün).
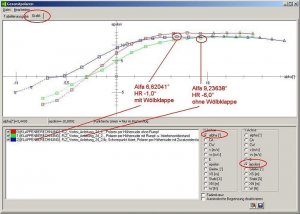
Das beste Gleiten in der grünen Kurve ergibt sich bei einem Anstellwinkel von etwa 4,8° und einem HR-Auschlag von -3°.
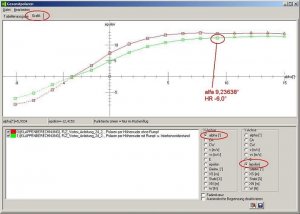
Steigzahl, auch Punkt des kleinsten Sinkens:
Bild 128
Für die Y-Achse wählen wir hier 'epsilon' für die Steigzahl.
Das beste Steigen in der grünen Kurve ergibt sich bei alfa = 9,23638° und einem HR-Ausschlag von -6.0°. Hier könnte man allerdings auch gut den Punkt links daneben nehmen, um ein wenig mehr Luft bis zum Strömungsabriss zu haben. Der Unterschied bei der Steigzahl ist minimal.
Untersuchung mit einer Zusatzklappe (Wölbklappe).
In das File Anhang anzeigen FLZ_Vortex_Anleitung_25.flz habe ich in der Mitte des Tragflügels eine Wölbklappe (hier Klappengruppe 19 , blaue Farbe) eingebaut. Ich möchte nun eine Polarenrechnung mit gesetzter Wölbklappe bei +10° ausprobieren.
Wir gehen zurück in die Karte 'Gesamtpolaren berechnen' und wählen den Tragflügel als aktiv und ziehen mit der rechten Maustaste die Wölbklappe in die zweite Listenzeile. Hier tragen wir für 'min. Winkel' und 'max. Winkel' fix 10° ein, des Weiteren erhöhen wir den 'min. Winkel' des HRs von +5° auf +10° und ändern die Anzahl der Schritte auf 20.
Bild 129
Wir starten nun die Berechnung und geben als Info-Text ein: 'Polaren per Höhenruder mit Zusatzwiderstand und Wölbklappe 10°'.
Das Programm wird nun die Wölbklappe auf +10° fest einstellen, da 'min. Winkel' und 'max. Winkel' den gleichen Wert haben und zwar für alle berechneten HR-Ausschläge.
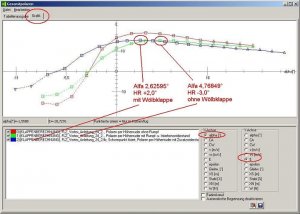
Wenn das Programm fertig ist, einmal den Button 'Gesamtpolaren anzeigen' anklicken und dann direkt in die Grafik gehen.
Gleitzahl (E):
Bild 130
Ein wirkliche Verbesserung der Gleitzahl ist nicht zu erkennen, wir haben lediglich die Polarkurve durch die Wölbklappe verschoben. Das beste Gleiten mit 10° Wölbklappe finden wir nun bei alfa = 2,62595° und einem HR-Ausschlag von +2.0°.
Steigzahl:
Bild 131
Auch bei der Steigzahl gibt es keine großen Verbesserungen (nur geringfügig, aber nicht das Gelbe vom Ei), sondern nur eine Verschiebung der Polaren.
Der Trainer ist nun mal kein gutes Segelflugzeug. Eine wirklich Verbesserung von Gleit- und Steigzahl bekommt man nur, wenn man die Streckung des Flügels erhöht und somit den induzierten Widerstand kleiner macht.
[PAGE][/PAGE]
11) Gesamtpolarenrechnung per EWD
Ich hatte ja schon angedeutet, dass man eine HR-Trimmung auch durch eine EWD ersetzten kann.
Hat man ein Pendel-HLW, dann könnte man entweder eine Polarenrechnung per Klappe oder EWD durchführen.
Hier wollen wir eine Polarenrechnung per EWD-Änderung durchführen.
Achtung:
Bei der EWD-Polarenrechnung werden bei den in der Liste eingetragenen Flügeln nur die Einstellwinkel geändert.
Voreingestellte Klappenausschläge (z. B. bei Wölbklappen oder Höhenrudern) bleiben erhalten.
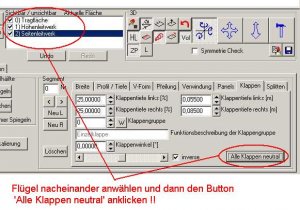
Möchte man eine reine EWD-Änderung der Flügel berechnen, so sollte man zuvor alle vorhandenen Klappen auf neutral (Klappenausschlagwinkel = 0°) stellen .
Bild 132
Wir laden unser Trainermodell Anhang anzeigen FLZ_Vortex_Anleitung_26.flz, in das ich die zusätzlichen Widerstände eingebaut habe.
Nun gehen wir in die Karte 'Gesamtpolaren berechnen' und hier in die Unterkarte 'EWD-Berechnung'. Der weiter Ablauf ist ähnlich dem der Klappenberechnung, nur dass wir diesmal keine Klappengruppen, sondern Flügelnummern in die Liste eintragen.
Wir wählen des HLW (Flügel Nr.1) aus und tragen eine '1' in die erste Zeile der Liste ein. Alternativ kann man wieder den Flügel mit der rechten Maustaste in die Liste ziehen (drag und drop). Für die Eckwerte des zu untersuchenden Einstellwinkelbereichs nehmen wir +5° und -5° an und tragen diese Werte bei 'min. Winkel' und 'max. Winkel' ein. Für die Anzahl der Schritte habe ich diesmal 20 gewählt, um eine etwas feinere Auflösung der Polaren zu erreichen.
Nun den Button 'Berechnung starten' drücken und als Info "EWD-Rechnung mit HLW" eintragen.
Bild 133
Nachdem das Programm fertig ist, drücken wir wieder den Button 'Gesamtpolaren anzeigen' und schauen uns die Tabelle an.
Bild 134
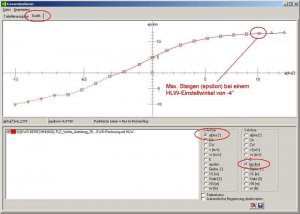
Ein in Normalfluglage fliegbarer Bereich würde sich hier für HLW-Einstellwinkel von +1° bis -4° ergeben.
Der Punkt für das beste Gleiten (E) liegt bei einem Einstellwinkel von -2° für das HLW.
Da der Einstellwinkel der Tragfläche in der Grundkonstruktion 0° beträgt, ergibt sich eine EWD von 2° für das beste Gleiten.
Den Einstellwinkel -4° für das beste Steigen (epsilon) würde ich allerdings nicht nehmen, weil...
- ...es keinen Spielraum mehr für eventuelle HR-Ausschläge nach oben gäbe.
Die einzige Steuermöglichkeit für andere Anstellwinkel wäre noch HR drücken. Das ist dann aber sehr gewöhnungsbedürftig. - ...das Modell (als Segler) in der Grundauslegung ohne Klappenausschläge ständig langsam (nahe am Strömungsabriss) unterwegs wäre und somit auch eine „leichte Beute“ für Böen.
Ich denke, ein guter Kompromiss wäre hier den Einstellwinkel -1,5° bis -2° zu wählen, um dann in der Thermik mit etwas HR-Zugabe in den Punkt des besten Steigens (kleinstes Sinken) zu trimmen.
Die Grafik für bestes Gleiten (E) sieht dann so aus:
Bild 135
Für das beste Steigen (epsilon) so:
Bild 136
[PAGE][/PAGE]
12) Import von Nurflügel-FLZ- und WinLaengs-Dateien
Der Import von Konstruktionsdaten, die mit anderen Programmen erzeugt wurden, ist nicht ohne Weiteres möglich.
Derzeit gibt es drei Dateiformate, die FLZ_Vortex importieren kann.
Das sind:
- FLG-Dateien (Programm Nurflügel),
- Da4-Dateien (Programm Winlaengs4 von Dietrich Meissner und Jörg Russow) und
- FLZ-Dateien (Programm FLZ_Vortex).
Im Prinzip könnte der Import auf weitere Dateiformaten erweitert werden. Auf der Wunschliste steht z. B. der Import von Dateien folgender Programme:
- XWing (Ulf Lehnert),
- AVL,
- XFLR5,
- Schwer.exe (Dietrich Meissner) und
- Schwerpunkt52.exe (Rainer Stumpf).
Also alle Konstruktionsdateien, in denen exakte Informationen zur Flugzeuggeometrie enthalten sind.
Wenden wir uns den vorhandenen Importfunktionen zu.
Beim Importieren wird eine bereits vorhandene Konstruktion im FLZ_Vortex nicht überschrieben!
Die importierten Daten werden dazu geladen.
Folgende Files möchte ich zur Demonstration benutzen:
- Anhang anzeigen H7.flg.flg
- Amigo III.da4 (Entnommen aus den Demo-Paket zu WinLaengs)
- Anhang anzeigen Tercel.flz (grob abgenommene Maße des Höllein-Seglers)
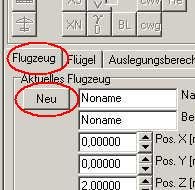
Wir starten das Programm FLZ_Vortex und erzeugen über die Karte 'Flugzeug' und den Button 'Neu' eine leere Szene.
Bild 137
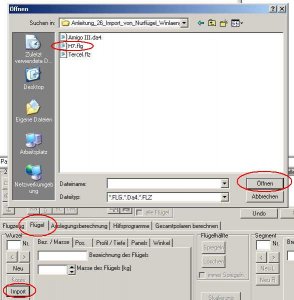
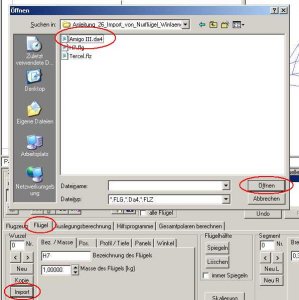
Nun wechseln wir in die Karte 'Flügel' und drücken den Button 'Import'. Es erscheint ein Dialogfenster, in dem alle Files mit den Endungen *.flg,*.flz,*.da4 angezeigt werden. Wir wählen zunächst das H7.flg.
Bild 138
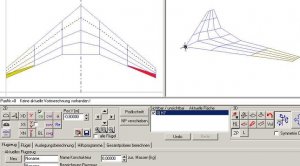
Nach dem Bestätigen sollte es im FLZ_Vortex so aussehen:
Bild 139
Feinheiten, wie die Panelauflösung in Spannweitenrichtung, sind hier nicht vorhanden, das muss noch nachgeholt werden, so wie wir das bereits gelernt haben.
Die Geometriedaten des Grundrisses sowie die Verwindung und die Klappendaten sind aber vorhanden.
Wir lassen diesen Flügel nun stehen und machen den nächsten Import mit dem File
Amigo III.da4:
Bild 140
In der 3D-Grafik sehen wir den zuerst geladenen Flügel H7 und zusätzlich den Segler Amigo.
Dieser wurde versetzt eingefügt, um Überschneidungen zu vermeiden.
In den Winlaengs-DA4-Dateien gibt es, wie auch bei den FLG-Dateien, keine Angaben zu V-Form oder zum SLW, deshalb sind alle Flügel platt.
Bei den Nurflügel-FLG-Dateien gibt es zumindest noch Profilangaben, die bei DA4-Dateien aber ebenfalls fehlen. Hier muss man also noch mehr per Hand nacharbeiten.
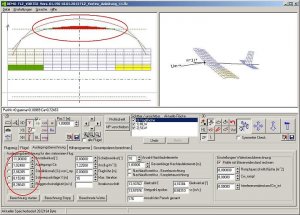
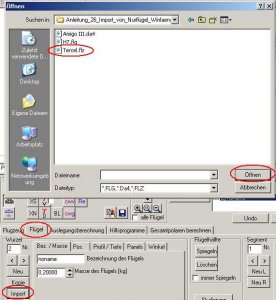
Zum Schluss importieren wir noch ein FLZ_Vortex-File: Tercel.flz.
Bild 141
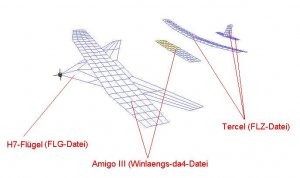
In der 3D-Grafik sieht es dann so aus:
Bild 142
Alle Flügel brauchen noch eine Bezeichnung und bis auf die Tercel-FLZ-Flügel eine mehr oder weniger aufwändige Nacharbeitung per Hand, weil ja Daten fehlen.
Da wir den Import nun kennen, könnte man auf den Gedanken kommen, sich eine Art Datenbank zu basteln, in der diverse Einzelflügel abgelegt werden.
- Verschiedene Segler-Flügel,
- verschiedene Seitenleitwerke oder Winglets und
- verschiedene HLWe.
Diese Einzelflügel könnten wir dann nach Belieben zu einem neuen Flugzeug zusammensetzen. Mit den Skalierungsmöglichkeiten des FLZ_Vortex können die Größen der Einzelflügel angepasst werden.
[PAGE][/PAGE]
13) Panelauflösung Flügelspitze (Randbogen)
Bis dato haben wir hauptsächlich die Bedienung und Funktionsweise der Eingabeelemente des FLZ_Vortex besprochen.
Hier soll es nun um die Panelauflösung gehen.
Während es bei den Segmenten um die Kontur eines Flügels geht (Konstruktion), werden die Panels für die Berechnung der Kräfteverteilung auf der Oberfläche benötigt. Je feiner man die Panelbelegung macht, um so besser kann man die Kräfte an bestimmten Punkten des Flügels berechnen. Das Ganze erfordert ein wenig Bauchgefühl und Erfahrung.
Zunächst einige grundlegende Vorbemerkungen:
Überall da, wo es zu großen Änderungen in der Geometrie kommt, sollte man die Panelauflösung verfeinern. Das wäre zum Beispiel an...
- ...Flügelspitzen (Randbogen).
Hier kommt es zum Druckausgleich zwischen der Ober- und Unterseite des Flügels. - ...Knicken des Flügels durch Pfeilung.
- ...Knicken des Flügels durch V-Form.
- ...Stellen, wo sich Rumpf und Flügel nahe kommen, wenn man einen Rumpf durch eine Fläche simuliert.
- ...Stellen, wo sich Klappen befinden. Hier entsteht durch den Klappenausschlag ein Knick in der Profilkontur und häufig auch eine zusätzliche Öffnung (Spalt) zwischen der Klappe und dem feststehenden Flügelteil.
File: Anhang anzeigen Panelbelegung_1.flz
Ich habe in Spannweitenrichtung eine Panelauflösung von 1, je Flügelhälfte ein Segment und auch in Flügeltiefenrichtung nur 1 Panel eingebaut.
Bild 143
Unsere Panelauflösung besteht in diesem Beispiel also nur aus zwei Panels.
Damit machen wir nun eine Anstellwinkelrechnung mit 5° und schauen uns die Zirkulationskurve an. Die Zirkulationswerte können als eine Art Kräfteverteilung angesehen werden, weil bereits die Fläche des Panels berücksichtigt wird. Zu einer Kraft in Newton wird es aber erst dann, wenn man den Staudruck mit einbezieht, in dem bekanntlich die Geschwindigkeit und Luftdichte enthalten ist. An der Form der Zirkulationskurve ändert sich durch den Staudruck aber nichts.
Bild 144
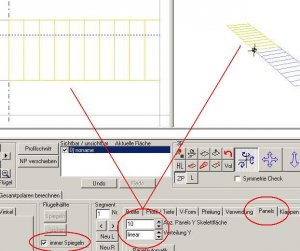
Diese Kurve ist jedoch völlig unbrauchbar, da man nur zwei Zirkulationswerte hat, jeweils für die Mitte der Panels in Spannweitenrichtung. Was an anderen Stellen entlang der Spannweite los ist, kann man nicht erkennen. Wir verfeinern deshalb die Panelauflösung in Spannweitenrichtung auf 10 Panels mit linearer Verteilung.
Bild 145
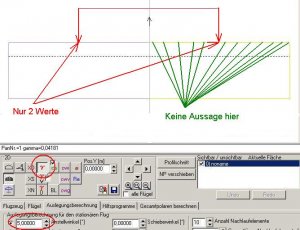
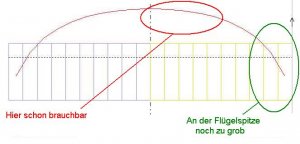
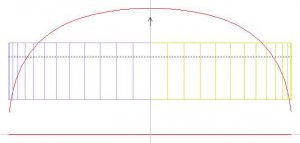
Wir führen eine erneute Anstellwinkelrechnung mit 5° durch. Das Resultat sieht schon deutlich besser aus, bis auf die Flügelspitze.
Bild 146
Man könnte nun hingehen und die Anzahl der Panels mit linearer Verteilung weiter erhöhen.
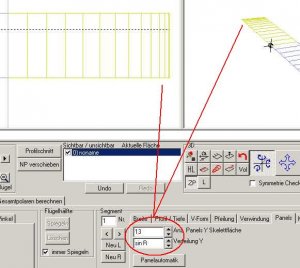
Wir könnten natürlich auch die sin_R - Funktion (Sinus-Rechts fein) nutzen. Machen wir’s doch...
Bild 147
Nun ist die Kurve bis fast zur Flügelspitze schön gleichmäßig.
Bild 148
Man kann die Anzahl der Panels natürlich weiter erhöhen. Falls sich aber bei den Ergebniswerten kaum noch etwas ändert, sollte man es gut sein lassen.
Die Anzahl der Panels erhöht zwangsläufig die Zeit für die Berechnung! Sobald sich beim Runden des Gesamt-CAs an der zweiten Stelle hinter dem Komma kaum noch etwas ändert, ist es für mich gut genug.
[PAGE][/PAGE]
14) Panelauflösung an Flügel mit Pfeilungsknicken
Nun geht es um die Problemstellen, an denen sich sprunghafte Pfeilungsänderungen in der Geometrie ergeben. Es gibt zwei Arten von Pfeilungen.
- Die positive Pfeilung: Es wird eine Flügelhälfte oder auch nur Teile (Segmente) der Flügelhälfte nach hinten gepfeilt -> positives Vorzeichen beim Pfeilungswinkel.
- Die negative Pfeilung: Es wird eine Flügelhälfte oder auch nur Teile (Segmente) der Flügelhälfte nach vorne gepfeilt -> negatives Vorzeichen beim Pfeilungswinkel.
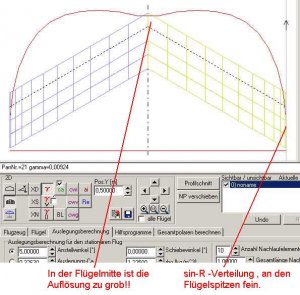
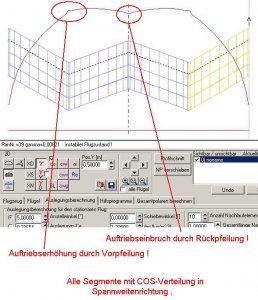
Hier wurde die Panelauflösung für die Flügelspitzen nach Anleitung 28 berücksichtigt. 11 Panels je Flügelhälfte in Spannweitenrichtung mit SIN-Verteilung und der Flügel wurde mit einem festen Anstellwinkel von 5° berechnet.
Bild 149
Am Kurvenverlauf erkennt man, dass durch die Pfeilung ein Einbruch der Zirkulationskurve (quasi die Kräfteverteilung) in der Flügelmitte entsteht. Die Knickstelle ist also ein Ort, an dem man die Paneldichte erhöhen sollte, weil man hier sonst zu grob rechnet.
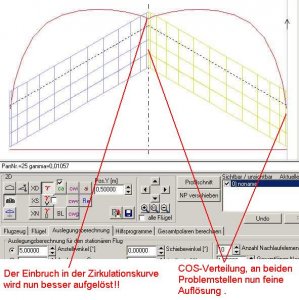
Im nächsten Bild habe ich daher die SIN-Verteilung durch eine COS-Verteilung ersetzt und die Zahl der Panels je Flügelhälfte von 11 auf 13 erhöht und erneut mit einer festen 5°-Anstellung gerechnet.
Bild 150
Jetzt wird die Zirkulationskurve an der Problemstelle in der Flügelmitte besser erfasst.
Pfeilung nach vorne:
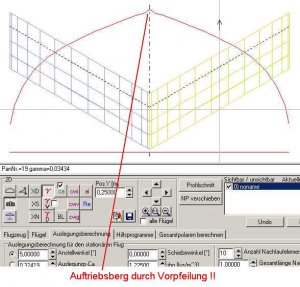
Wir nehmen den Flügel aus dem letzten Bild und versehen den Pfeilwinkel mit einem negativen Vorzeichen, also -30°. Auch diesmal rechnen wir wieder mit dem Anstellwinkel von 5°.
Bild 151
Anstelle des Auftriebseinbruches haben wir nun einen Auftriebsberg in der Flügelmitte.
Es kann auch Kombinationen von Vorwärts- und Rückwärtspfeilungen geben. In diesen Fällen ist die Verfeinerung der Panelbelegung an jeder Knickstelle erforderlich.
Bild 152
Man kann nun Versuche anstellen und die Panelzahl kontinuierlich erhöhen. Wie oben bereits erwähnt, ist eine weitere Erhöhung der Panelanzahl dann nicht mehr sinnvoll, wenn sich das Ergebnis (z. B. das Gesamt-CA) kaum noch ändert.
[PAGE][/PAGE]
15) Panelauflösung an Flügel mit V-Form
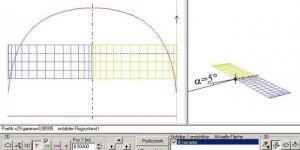
Auch eine V-Form erzeugt, ähnlich wie eine Pfeilung, einen Auftriebsberg bzw. einen Auftriebseinbruch. Man sollte also auch dort, wo sprunghafte V-Formänderungen in der Geometrie des Flügels vorhanden sind, eine Verfeinerung der Panelverteilung vorsehen. Dies soll am folgenden Beispiel demonstriert werden.
Die folgenden Bilder zeigen zunächst einen Flügel ohne V-Form:
Bild 153
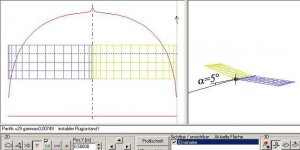
Nun ein Flügel mit 5° positiver V-Form (je Flächenhälfte), also Flügelenden nach oben:
Bild 154
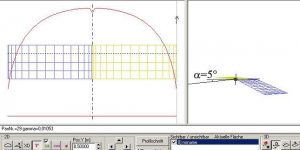
Diesmal mit -5°, also mit negativer V-Form:
Bild 155
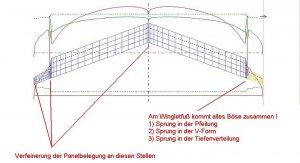
Die Panelbelegung in der Flügelmitte und an den Flügelspitzen wurde hier mit Hilfe der COS-Verteilung in Spannweitenrichtung verfeinert. Der gesamte Flügel hat einen konstanten Anstellwinkel von 5°.
Man sieht, dass wieder der Bereich in der Flügelmitte betroffen ist. Starke V-Form-Sprünge sind z. B. im Bereich von Flügel->Winglet-Übergängen zu finden oder auch beim V-Leitwerk. Beim Winglet kommt häufig auch noch eine sprunghafte Pfeilung und ein Sprung in der Tiefenverteilung hinzu. Daher sollte in diesen Fällen mit einer feineren Panelbelegung gearbeitet werden.
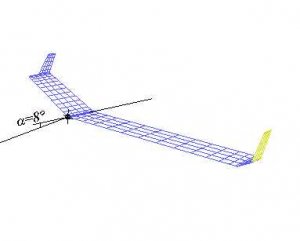
Hier noch ein weiterer Demo-Nurflügel, gerechnet mit einem festen Anstellwinkel von 8°.
Anhang anzeigen Anleitung_30.flz
Diesen bitte jetzt nicht unbedingt nachbauen! Es soll damit nur gezeigt werden, wo überall kritische Stellen auftauchen können.
Bild 156
Bild 157
[PAGE][/PAGE]
16) Panelauflösung in Tiefenrichtung X
Jetzt geht es um die Panelbelegung in Profiltiefenrichtung.
In der Anleitung 'Die erste Aerodynamik-Rechnung, Vorbereitung' haben wir diese Eingabefunktion schon einmal benutzt, ohne aber dabei auf die Auswirkungen bezüglich Flugeigenschaften einzugehen.
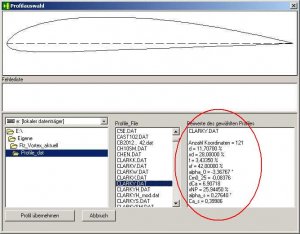
Bei der Auswahl eines neuen Profils haben wir sicherlich schon einmal einen Blick auf die Tabelle 'Beiwerte des gewählten Profiles' geworfen.
Bild 158
Die Spezialisten unter uns können mit den Werten sicherlich etwas anfangen, Anfänger sind allerdings damit bestimmt überfordert, vermute ich mal.
Diese Profilbeiwerte sind mit der Thin-Airfoil-Theorie (TAT) berechnet worden. Mit dieser Rechenmethode lassen sich ohne großen Aufwand recht schnell wichtige Profilbeiwerte (z. B. Alfa0 = Nullauftriebswinkel, cm0 = Nullmomentenbeiwert) berechnen. Das Profil wird bei diesem Verfahren auf die sogenannte Skelettlinie reduziert. Das ist die Linie, die genau auf der Hälfte zwischen Profilober- und Unterseite zu finden ist.
Diese Sklettlinie wird nicht nur bei den Traglinienverfahren sondern auch bem Vortex-Lattice-Verfahren benutzt. Hier durch ein Aneinanderreihen von Skelettlinien in Spannweitenrichtung. Dadurch entsteht die Skelettfläche, die wir immer dann sehen können, wenn man in der 3D-Grafik den Button 'VOL (Volumendarstellung) abschaltet. Die Außenkontur des Profils wird also in der Vortex-Lattice-Rechnung ignoriert.
Die TAT vernachlässigt die Reibung. Der Widerstand, der beim realen Flug existiert, wird nicht mitberechnet. Der Widerstand eines Profils entsteht durch die Wirkrichtung der Kraftvektoren entlang der Profilkontur. In großen Teilen auch durch Kräfte in der Grenzschicht, die sich nahe der Profiloberfläche bildet. Die Grenzschicht kann man sich wie einen Klebefilm aus Luft vorstellen. Teile der Grenzschicht (Luftteilchen nahe am Profil) werden festgehalten und andere Teilchen, weiter außen, können sich frei bewegen.
In der Grenzschicht entstehen so Scherkräfte, die Widerstand erzeugen. Irgendwann sind die Scherkräfte so groß, dass die Grenzschicht zerreißt und es zu Ablösungen kommt. Es können Blasen entstehen oder auch eine totale Ablösung (Strömungsabriss).
Bei großen RE-Zahlen (RE-Zahl = Profiltiefe [m] * Geschwindigkeit[m/s] * 70000) passen die Beiwerte der TAT ganz gut. Bei kleinen RE-Zahlen, wie sie im Modellflug üblich sind, kann es leider zu großen Abweichungen zwischen den TAT-Beiwerten und den Praxis-Beiwerten kommen, dazu aber später in einer anderen Anleitung mehr.
Hier soll es erst mal darum gehen, wie die Profilbeiwerte überhaupt in die Konstruktion einbezogen werden können.
Eine Idee wäre:
Einfach an allen Stützstellen (Profiltiefenrichtung X) die Profilkontur oben und unten nehmen und daraus die Skelettlinie basteln.
Also z_skelett(X) = ( z_oben(X) + z_unten(X) ) / 2.
Das funktioniert auch gut, wenn man sehr viele Stellen (80, 90 oder100 Stellen) in Tiefenrichtung hat. Man muss aber dann bedenken, dass man ja auch in Spannweitenrichtung sehr viele Panels hat und auf diese Weise hunderte Panels für die gesamte Konstruktion entstehen. Die Rechenzeit würde dann enorm lang, aber wir haben es ja immer eilig.
Ich möchte an einem Beispiel diesen Weg dennoch einmal aufzeigen.
Der Tabelle oben entnehmen wir die Werte:
alfa_0 = -3,36767°
und
Cm0_25 = -0,08376
für das Profil Clarky.dat heraus.
alfa_0 ist der Anstellwinkel, bei dem das Profil keinen Auftrieb mehr liefert.
Cm0_25 ist der Nick-Momentenbeiwert um die t/4-Linie bei Null_Auftrieb.
Die 25 steht für Drehpunktstelle bei 25% der Profiltiefe = t/4-Linie.
Obwohl bei CA = 0 kein Auftrieb entsteht, erzeugt das Profil Clarky dennoch ein Nickmoment.
In Bezug auf den Auftrieb heben sich alle Kräfte rund um das Profil auf.
Die Kräfte sind aber so verteilt, dass hinter der t/4-Linie mehr Kraft erzeugt wird als vor der t/4-Linie. Somit ergibt es ein Nickmoment nach vorne unten.
Die t/4-Linie ist bei fast allen Profilen auch der Neutralpunkt (bei den Beiwerten in der Tabelle oben der Wert xNP) des Profils. Wenn man einen Schnelldurchlauf durch die Profile macht und sich den Wert xNP anschaut, wird man feststellen, dass dieser Neutralpunkt meist so zwischen 24%, 25% und 26% hin und her eiert. Dieser Sachverhalt ist schon ziemlich erstaunlich und überraschend. Daher hat es sich als sinnvoll erwiesen, den Profilmomentenbeiwert auf die 25%-Linie = t/4-Linie zu beziehen .
Wie kann man nun überprüfen, ob eine im FLZ_Vortex eingebaute Panelbelegung in Profiltiefenrichtung auch die Profilbeiwerte des Profils richtig abbildet?
Um diese Frage zu beantworten, müssen wir uns einen Experimentalflügel basteln.
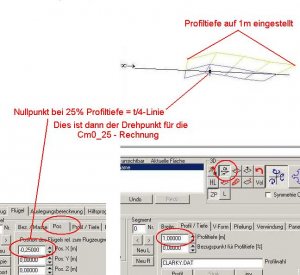
Wir erzeugen dazu ein neues Flugzeug und einen neuen Flügel. Darin bauen wir das Profil Clarky in die Flügelwurzel und in die Segmente ein. Unsere Profildateien '*.dat' sind auf eine Länge von 1 normiert. Länge 1 ist schön neutral und lässt sich direkt auf jede andere Länge skalieren. Der Testflügel hat aber default eine Profiltiefe von 0,2 m, diese ändern wir auf 1 m ab. Also die Wurzel-Profiltiefe beträgt 1 m und die Segment-Profiltiefen stellen wir auf 1m ein.
Danach gehen wir in die Karte 'Wurzel', dort in die Unterkarte 'Pos.' und ändern die Position des Flügels, indem wir in das Editfenster 'Pos.X' den Wert -0,25 m eintragen. Der Nullpunkt des Flügels wird damit auf die t/4-Linie (25%-Linie) des Flügels verschoben. Dies hat den Zweck, dass wir nach einer Vortexrechnung einen Profil-Momentenbeiwert bekommen, der auf die t/4-Linie bezogen ist, genau wie oben in der TAT-Tabelle. Somit können wir die Momentenbeiwerte (Cm0 der TAT und Cm0 aus Vortex) direkt vergleichen
Bild 159
File: Anhang anzeigen Anleitung_31_1.flz
Nun kommt noch eine Kleinigkeit.
Die Spannweite ist mit 1 m viel zu klein. Vortex rechnet eine Umströmung der Flügelspitze und der entstehende Randwirbel würde alles verfälschen. Der Einfluss des Randwirbels muss auf nahe 0 eliminiert werden. Das können wir nur erreichen, indem wir eine extrem große Spannweite erzeugen und so die Flügelspitze quasi ins Unendliche schieben. Wir geben deshalb für die Flügelbreite je Segment 10.000 m ein, das dürfte die Flügelspitze weit genug verschieben.
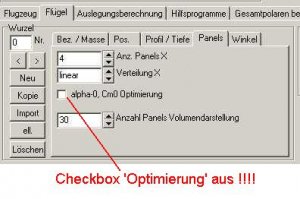
Noch eine weitere Winzigkeit und wir können mit den Berechnungen loslegen.
Dazu müssen wir in die Karte 'Flügel', Unterkarte 'Panels' wechseln und hier den Checkbutton 'alfa-0, Cm0 Optimierung' ausschalten. Dahinter verbirgt sich eine Routine, die es erlaubt , auch mit wenigen Panels in Tiefenrichtung die Profil-Beiwerte alfa0 und cm0 abzubilden. Ist dieser Button aus, dann wird die Skelettlinie im Vortex aus den Originalprofildaten der Ober- und Unterseite gebildet.
Bild 160
Im File Anhang anzeigen Anleitung_31_2.flz habe ich alle bisher erwähnten Einstellungen eingefügt.
Im Augenblick haben wir in Flügeltieferichtung eine Paneleinstellung von vier Panels mit linearer Verteilung.
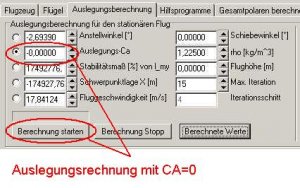
Wir machen nun eine Nullauftriebsrechnung und schauen uns die Profilbeiwerte an, die FLZ_Vortex ohne Optimierung daraus zaubert.
Nun wechseln wir in die Karte 'Auslegungsrechnung', fixieren den Radiobutton vor dem Editfeld 'Auslegungs-CA' und berechnen den Flügel mit CA = 0.
Bild 161
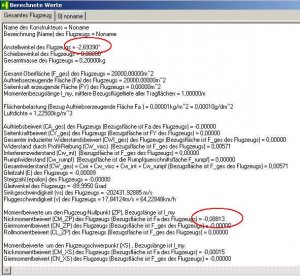
Dann drücken wir den Button 'Berechnet Werte' und schauen uns hier die Werte für den
Anstellwinkel des Flugzeuges = -2,6939° (Alfa0)
und den
Nickmomentbeiwert (CM_ZP) des Flugzeugs (Bezugsfläche ist Fa des Flugzeugs) = -0,08813 (Cm0_25) an.
Bild 162
Vergleich:
TAT_Alfa0 = -3,36767°
Vortex_Alfa0 = -2,6939°
TAT_Cm0 = -0,08376
Vortex_Cm0 = -0,08813
Die Unterschiede sind doch recht deutlich.
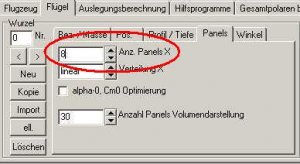
Wir verdoppeln nun die Anzahl der Panels auf acht in X-Tiefenrichtung und machen dann eine erneute CA = 0-Berechnung.
Bild 163
Vergleich (Werte stehen wieder in Karte 'Berechnete Werte'):
TAT_Alfa0 = -3,36767°
Vortex_Alfa0 = -3,04951°
TAT_Cm0 = -0,08376
Vortex_Cm0 = -0,08733
Die Werte nähern sich an.
Nun wird die Anzahl der Panels weiter erhöht.
Bei 128 Panels in X-Tiefenrichtung ergeben sich folgende Resultate:
TAT_Alfa0 = -3,36767°
Vortex_Alfa0 = -3,35004°
TAT_Cm0 = -0,08376
Vortex_Cm0 = -0,08422
Jetzt passt es so halbwegs, wurde aber mit einer enorm langen Rechenzeit erkauft.
Nun schalten wir den Checkbutton 'alfa-0, Cm0 Optimierung' wieder ein und reduzieren die Anzahl der Panels in X-Tiefenrichtung wieder auf vier und machen eine erneute CA = 0-Rechnung.
Vergleich bei vier Panels mit Optimierungs-Funktion:
TAT_Alfa0 = -3,36767°
Vortex_Alfa0 = -3,34698°
TAT_Cm0 = -0,08376
Vortex_Cm0 = -0,08374
Dann noch mal mit acht Panels und Optimierung:
TAT_Alfa0 = -3,36767°
Vortex_Alfa0 = -3,35554°
TAT_Cm0 = -0,08376
Vortex_Cm0 = -0,08397
Wir sehen, die eingebaute Optimierungsfunktion liefert schon bei wenigen Panels in Tiefenrichtung sehr brauchbare Ergebnisse und sollte daher immer aktiv geschaltet bleiben.
Bei S-Schlagprofilen sieht die Sache noch viel extremer aus. Dort braucht man für eine Rechnung ohne Optimierung'immer' enorm viele Panels (>100) in Tiefenrichtung, weil sonst die stabilisierende Eigenschaft der hinteren Wölbung nicht richtig erfasst werden kann.
Probiert das einfach mal aus und ersetzt das Clarky z. B. durch ein Clarkys.dat, dies ist ein S-Schlag-Profil, das z. B. beim Brettnurflügel verwendet werden kann.
<ca. 9000 Worte>